More Information
Submitted: November 25, 2022 | Approved: December 20, 2022 | Published: December 30, 2022
How to cite this article: Vishwanathan K. Au26-35: A Special Geometrical Structure of Au33 (D2) Cluster with Highly Occupied - 14 Pairs of Double-State Degeneracy. Ann Adv Chem. 2022; 6: 063-081.
DOI: 10.29328/journal.aac.1001035
Copyright License: © 2022 Vishwanathan K. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Gold atomic clusters; Density-Functional Tight-Binding (DFTB) approach; Finite-difference Method; Force Constants (FCs) and Vibrational spectrum
Au26-35: A Special Geometrical Structure of Au33 (D2) Cluster with Highly Occupied - 14 Pairs of Double-State Degeneracy
K Vishwanathan*
Faculty of Natural Sciences and Technology, University of Saarland, 66123, Saarbrücken, Germany
*Address for Correspondence: K Vishwanathan, Faculty of Natural Sciences and Technology, University of Saarland, 66123, Saarbrücken, Germany, Email: [email protected]; [email protected]
In this article, an interesting phenomenon has described the geometries and vibrational frequency of the stable Aun clusters with n = 26 to 35. We have found nine out of ten clusters are having the very same C1 symmetry, except the cluster n = 33 (D2). The finite-differentiation method has been implemented within the density-functional tight-binding (DFTB) approach. The effects of the range of interatomic forces were calculated and the desired set of system eigenfrequencies (3N-6) are obtained by diagonalization of the symmetric positive semidefinite Hessian matrix. Mainly, we have observed the vibrational spectra and the range comes in between 2.04 and 347.32 cm−1 at ground state, ∆E = 0. Most significantly, all the clusters have revealed double-state degeneracy. The vibrational spectrum is strongly dependent upon the size, shape, and structure, at the same time, the stretching and the bending mode of the atoms with respect to the bond length plays a major role. We have compared some of our results, which have an excellent agreement, with the less availability of the experimental and the theoretical predictions.
In the past decades, gold clusters have attracted the great interest of both experimental and theoretical researchers due to their fundamental importance and tremendous potential applications in catalysis, biology, and nanoscale devices [1-12].
In general, noble-metal (Cu, Ag, and Au) clusters have attracted much attention in scientific and technological fields because of their thermodynamic, electronic, optical, and catalytic properties in nano-materials [13-15]. Especially, gold is a soft metal and is usually alloyed to give it more strength as well as a good conductor of heat and electricity, and is unaffected by air and most reagents, those are the main reasons to choose among the other metal clusters. Its physical and chemical properties appear to be entirely changing as the size of metal continuously decreases into the nanoscale because of the quantum size effect, surface effect, small size effect, and macroscopic quantum tunneling (MQT) effect [16, 17].
Nanotechnology is a relatively new branch of science that has found a wide range of applications that range from energy production to industrial production processes to biomedical applications [18]. One of the key applications is in biology and biomedical research. Nanoparticles (NPs) can be engineered to possess unique compositions and functionalities, which can provide novel tools and techniques that, have not previously existed in biomedical research. For example, NPs can be used to image biological processes on the cellular level. They can also be utilized to detect analytes at the attomolar range [19].
Nanotechnology has become a trending area in science and has made great advances with the development of functional, engineered nanoparticles. Various metal nanoparticles have been widely exploited for a wide range of medical applications. Among them, gold nanoparticles (AunPs) are widely reported to guide an impressive resurgence and are highly remarkable. AunPs, with their multiple, unique functional properties, and ease of synthesis, have attracted extensive attention. Their intrinsic features (optics, electronics, and physicochemical characteristics) can be altered by changing the characterization of the nanoparticles, such as shape, size, and aspect ratio. They can be applied to a wide range of medical applications, including drug and gene delivery, photothermal therapy (PTT), photodynamic therapy (PDT) and radiation therapy (RT), diagnosis, X-ray imaging, computed tomography (CT), and other biological activities [20].
Particularly, gold nanoclusters (AunCs) have been extensively applied as fluorescent probes for biomedical applications in imaging, detection, and therapy due to their unique chemical and physical properties [21]. Recently, reported that gold phosphine complexes show anticancer activity toward a panel of different tumor cell lines [22]. In addition, gold clusters with near-infrared II (NIR-II) fluorescence are used to monitor high-resolution imaging of kidneys at a depth of 0.61 cm, and the quantitative measurement shows 86% of the gold clusters are cleared from the body without any acute or long-term toxicity at a dose of 100 mg kg−1. Bright gold clusters can penetrate deep tissue and can be applied in vivo brain vessel imaging and tumor metastasis [23].
In recent years, gold compounds have gained more and more attention in the design of new metal anticancer drugs. Numerous types of research have reported that gold compounds, in addition to their widely studied cytotoxic antitumor effects, also reverse tumor immune escape and directly facilitate the functions of immune cells, leading to enhanced anticancer effects [24].
Gold clusters, which display a variety of unusual geometric structures due to their strong relativistic effects, have attracted much attention. Among them, Au26 has a high-symmetry tubular structure (D6d) with a large HOMO-LUMO energy gap, but its electronic stability still remains unclear. In Liu Q, et al. paper, the electronic nature of the Au26 cluster is investigated using the density functional theory method. Depending on the super valence bond model, the tubular Au26 cluster with 26 valence electrons could be viewed as a super atomic molecule composed of two open cages based on spherical aromaticity, and its molecule-like electronic shell closure is achieved via a super triple bond (σ, 2π) between the two cages [25].
Gold clusters are known to form many cages like geometries such as Au20, Au24, and Au32. The shape of these clusters varies from Tetrahedral (Au20) cage to Fullerene like (Au32) and tubular form (Au24) [26]. The Au26 cluster is one of the widely studied gold clusters in the size range of n = 21-30. It has been proposed in a more recent combined experimental and theoretical study that the neutral Au26 cluster is fluxional. The fluxionality of a cluster is relevant to its catalytic applications [27]. The structural evolution of negatively charged gold clusters (Aun-) in the medium size range for n = 27-35 has been investigated using photoelectron spectroscopy (PES) and theoretical calculations by the research group of Nan Shao, et al. [27]. The cage-like gold clusters would be of both fundamental and practical interest because of their high surface area (all the atoms are on the cluster surface) and hollow cavity to accommodate other atoms or molecules [28].
A surprising stability of the tube-like Aun (n = 26-28) has been shown using the scalar relativistic all-electron density functional theory calculations, forming another powerful candidate for the lowest-energy Aun competing with those previously suggested space-filled structures. Unlike the icosahedral “golden” fullerene Au32, these tube-like gold clusters may be closely related to the synthesized single-wall gold nanotubes (SWGNT). The ground-state Au26 has a hollow tube-like structure constructed from the (6, 0) SWGNT, yielding a high-symmetry D6d cage, based upon which the most stable Au27 and Au28 can be obtained by capped one and two atoms, respectively [29]. In total, gold is a multipurpose material that has been utilized for examining technological applications [30].
DFTB-based global searches have not been done for gold clusters in the range of Au26 to Au35. Structural determination for larger gold clusters becomes increasingly more challenging, and global minimum searches are essential because of the sheer number of possible atomic arrangements. Except for Au32- and Au34-. In fact, the global minima of Au32- and Au34- are still controversial [31 - 37].
Most recently, Philipp Gruene, et al. have calculated, vibrational spectra of small neutral gold clusters containing up to 8 Au atoms which were measured in the far-infrared (46-222 cm-1) via photodissociation of their complexes with krypton atoms. They have compared with calculated IR spectra for bare Au𝑛 clusters using density functional theory that has allowed for structural assignment. For those small sizes, all clusters are found to be planar and of comparably high symmetry [38]. Therefore, with the highest possible, the vibrational properties could be able to calculate with the help of Infrared Intensity and partial Infrared Intensity [30]. Additionally, vibrational spectroscopy was utilized for analyzing the gold cluster structures and DFT calculations were used for the investigations of small complex gold clusters [39]. The theoretical studies on the electronic, optical, vibrational, and other physical and chemical properties of the gold clusters are at the forefront of cluster science [40].
Gold has been the major focus of the SCC-DFTB field due to its promising applications in the development of new nanodevices [41]. Moreover, the DFTB method has been utilized to design these gold clusters which are size-dependent and it is observed that quantum confinement effects narrowed the energy gap [30].
In this study, we focus mainly on the vibrational properties of gold atomic clusters with sizes Au26-35 atoms, because it plays a major role in structural stability [42-49]. Further assistance for the readers, specifically for the general information about global minima gold structures which have been calculated by the work of Dong and Springborg can be found in those articles [50, 51]. In very short, the structures were found through a so-called genetic algorithm (GA) in combination with Density Functional Tight-Binding (DFTB) energy calculations and the steepest descent algorithm permitting a local total energy minimization. Nevertheless, in our case, we use the numerical finite-difference method [52] along with the density-functional tight-binding (DFTB) approach [53 - 55] and finally extract the vibrational spectrum from the re-optimized structures.
The following section introduces the DFTB procedures used for our calculations. Overall, the depth and detailed information are discussed in the results and discussion section.
Theoretical and computational procedures
In the first step, the DFTB [53 - 55] is based on the density functional theory of Hohenberg and Kohn in the formulation of Kohn and Sham. In addition, the Kohn-Sham orbitals ψi(r) of the system of interest are expanded in terms of atom-centered basis functions {φm(r)},
ψi(r) = (r), m = j. (1)
While so far the variational parameters have been the real-space grid representations of the pseudo wave functions, it will now be the set of coefficients cim. Index m describes the atom, where is centered and it is angular as well as radially dependent. The is determined by self-consistent DFT calculations on isolated atoms using large Slater-type basis sets.
In calculating the orbital energies, we need the Hamilton matrix elements and the overlap matrix elements. The above formula gives the secular equations
(2)
Here, cim’s are expansion coefficients, is for the single-particle energies (or where are the Kohn-Sham eigenvalues of the neutral), and the matrix elements of Hamiltonian Hmn and the overlap matrix elements Smn are defined as
(3)
They depend on the atomic positions and on a well-guessed density ρ(r). By solving the Kohn-Sham equations in an effective one-particle potential, the Hamiltonian is defined as
(4)
To calculate the Hamiltonian matrix, the effective potential Veff has to be approximated. Here, being the kinetic-energy operator and Veff(r) being the effective Kohn-Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,
(5)
is the Kohn-Sham potential of a neutral atom, rj = r-Rj is an atomic position, and Rj is the coordinates of the j atom.
Finally, the short-range interactions can be approximated by simple pair potentials, and the total energy of the compound of interest relative to that of the isolated atoms is then written as,
(6)
Here, the majority of the binding energy (∈i) is contained in the difference between the single-particle energies (∈i) of the system of interest and the single-particle energies ∈jmj of the isolated atoms (atom index j, orbital index mj), is determined as the difference betweenand ∈B and for diatomic molecules (with ESCF being the total energy from parameter-free density-functional calculations). In the present study, only the 5d and 6s electrons of the gold atoms are explicitly included, whereas the rest are treated within a frozen-core approximation [54 - 56].
Structural re-optimization process
This work is dedicated to the computational investigation of the gold clusters that vary with the number of atoms and becomes difficult for the computational investigation of gold clusters and required very precise and careful methodology with accuracy.
In our case, we have calculated the numerical first-order derivatives of the forces (Fiα, Fjβ) instead of the numerical second-order derivatives of the total energy (Etot). In principle, there is no difference, but numerically the approach of using the forces is more accurate [52].
Here, F is a restoring force that is acting upon the atoms, ds is a differentiation step-size and M represents the atomic mass, for the homonuclear case. The complete list of these force constants (FCs) is called the Hessian H, which is a (3N X 3N) matrix. Here, i is the component of (x, y or z) of the force on the j atom, so we get 3N. The Hessian matrix is the matrix of second derivatives of the energy with respect to geometry which is quite sensitive to its geometry. Energy second derivatives are evaluated numerically. The mass-weighted Hessian matrix is obtained by numerical differentiation of the analytical first derivatives, calculated at geometries obtained by incrementing, in turn, each of the 3N nuclear coordinates by a small amount of ds with respect to the equilibrium geometry. The introduction of the Hessian matrix and its diagonalization ultimately leads to the eigenfrequencies of the system and its eigenvectors, describing the harmonic motion of the cluster atoms. In order to obtain the matrix elements Hij of the Hessian matrix which is needed if one wishes to investigate the cluster’s thermodynamic properties and one should obtain the derivatives of potential energy surface (PES) [57].
The optimized structure of the clusters Au26-35
We present the vibrational spectrum analysis of the re-optimized Au26-35 clusters, interestingly, all of them are having the very same point group symmetry C1, except Au33 (D2), at ground state, ∆E = 0. Initially, the structures were found through a so-called genetic algorithm (GA) in combination with Density Functional Tight-Binding (DFTB) energy calculations and the steepest descent algorithm permitting a local total energy minimization [58, 59]. To sum up, we have accurately predicted the vibrational frequency of the clusters, and they are very strongly dependent on the size, structure, and shape of the clusters [60], as well as, mainly influenced by the stretching and the bending mode vibrations of the atoms that are due to changes on the bond length fluctuations for a small step-size ds = ± 0.01 a.u. on the equilibrium coordinates [61]. Importantly, these spectra are different for the different atomic configurations.
In brief, this study represents the first such one where also electronic degrees of freedom explicitly are included, which indeed turns out to be important. When including orbital interactions, not only packing but also directional interactions determine the optimal structure and, therefore, in most cases, our optimized structures do not have a very high symmetry, i.e., the occurrence of magic numbers becomes much less pronounced. In this respect, again, we would like to bring your attention to, an atom of gold that seems to be special. For other metals, packing effects are often dominating, whereas, for covalently bonded elements, the effects due to directional bonds are dominating. We suggest that for gold there is a competition between the two leading to the low-symmetry, although quite compact structures of the Aun (n = 2-58) clusters [58, 59]. By comparing with the results of jellium calculations, it was demonstrated that for gold clusters, electronic effects are very important, leading to a partial suppression of the occurrence of magic numbers, as well as to low-symmetry and less compact clusters.
In general, the IR bond gives information about the point group symmetry of structures [62,63]. Bonds that are formed in the near-infra-red range are considered the weaker ones. Far infrared spectroscopy is observed in the frequency region that is less than 10 cm−1 and responds to the stretching and bending mode of vibrations. In the experiment, generally not able to observe the silent modes that play a fundamental role in the intermolecular non-radiative energy transfer of energy and play a central role in the determination of stability of the gold clusters [30].
For the perspective view, we have plotted with two different styles (Space-filling, Polyhedral). Specifically, Figures 1-10, sharply show the standard orientation of the crystal shape of the clusters Au26-35 at ∆E = 0 (the lowest energy geometrical structure).
The vibrational frequency (ωi) range of the cluster Au26 at ∆E = 0
Table 1 shows the low (at the least) and the high (at the most) frequency range of the cluster Au26, which occurs between 6.58 and 319.61 cm−1, and the lowest energy geometrical structural view can be seen in Figure 1.
| Table 1: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au26 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 6.58 | 34 | 70.45 | 67 | 258.00 |
| 2 | 7.29 | 35 | 78.10 | 68 | 265.07 |
| 3 | 9.39 | 36 | 80.07 | 69 | 268.11 |
| 4 | 10.70 | 37 | 83.41 | 70 | 292.52 |
| 5 | 11.87 | 38 | 87.48 | 71 | 311.52 |
| 6 | 12.93 | 39 | 89.29 | 72 | 319.61 |
| 7 | 15.24 | 40 | 94.17 | 73 | - |
| 8 | 16.53 | 41 | 98.24 | 74 | - |
| 9 | 17.19 | 42 | 107.64 | 75 | - |
| 10 | 18.64 | 43 | 108.67 | 76 | - |
| 11 | 20.11 | 44 | 114.24 | 77 | - |
| 12 | 21.17 | 45 | 118.12 | 78 | - |
| 13 | 23.38 | 46 | 125.24 | 79 | - |
| 14 | 23.71 | 47 | 133.10 | 80 | - |
| 15 | 27.87 | 48 | 137.96 | 81 | - |
| 16 | 28.26 | 49 | 138.62 | 82 | - |
| 17 | 29.37 | 50 | 147.07 | 83 | - |
| 18 | 31.95 | 51 | 158.52 | 84 | - |
| 19 | 33.79 | 52 | 159.82 | 85 | - |
| 20 | 34.92 | 53 | 164.40 | 86 | - |
| 21 | 36.62 | 54 | 172.92 | 87 | - |
| 22 | 38.77 | 55 | 182.37 | 88 | - |
| 23 | 40.98 | 56 | 189.42 | 89 | - |
| 24 | 41.87 | 57 | 191.12 | 90 | - |
| 25 | 43.84 | 58 | 197.37 | 91 | - |
| 26 | 47.67 | 59 | 202.15 | 92 | - |
| 27 | 54.03 | 60 | 206.51 | 93 | - |
| 28 | 58.48 | 61 | 214.69 | 94 | - |
| 29 | 59.69 | 62 | 218.92 | 95 | - |
| 30 | 61.31 | 63 | 226.91 | 96 | - |
| 31 | 64.49 | 64 | 230.00 | 97 | - |
| 32 | 66.90 | 65 | 234.05 | 98 | - |
| 33 | 68.03 | 66 | 249.25 | 99 | - |
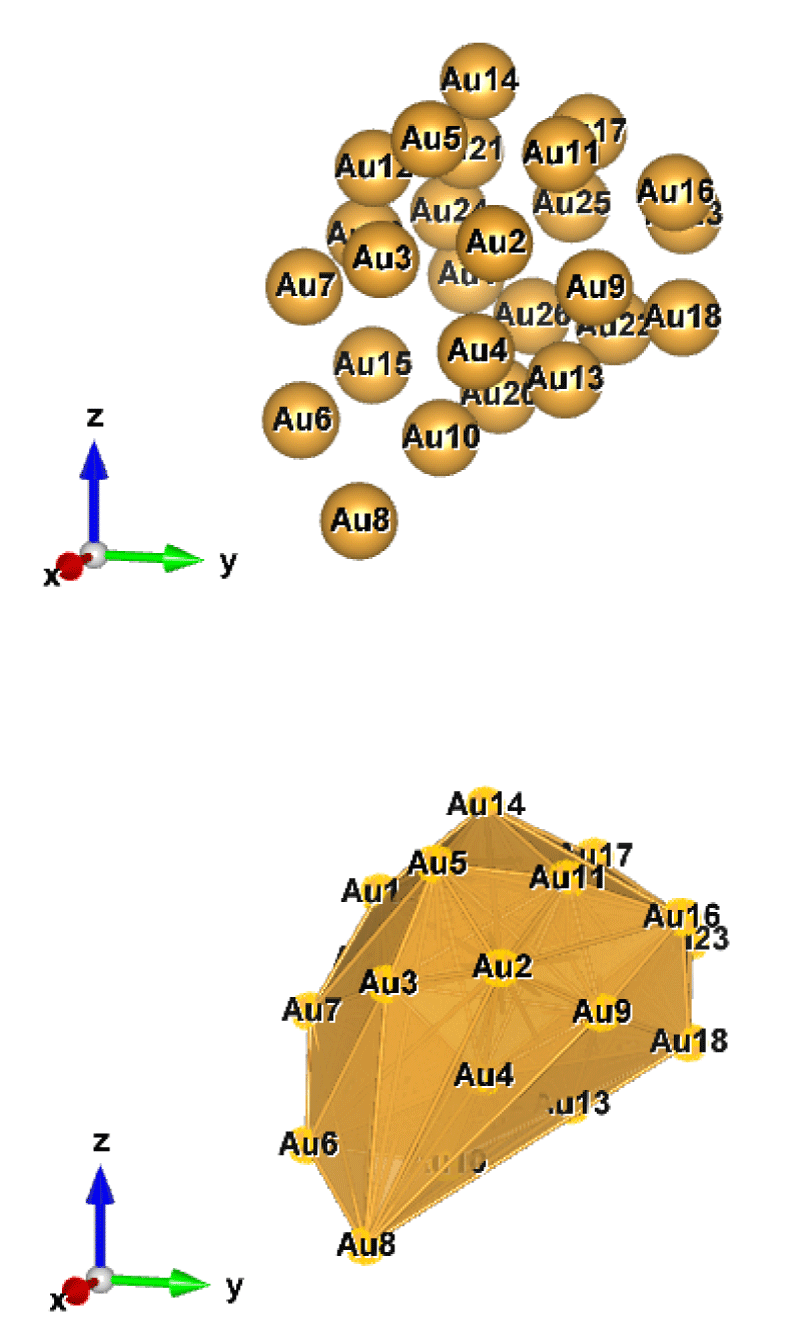
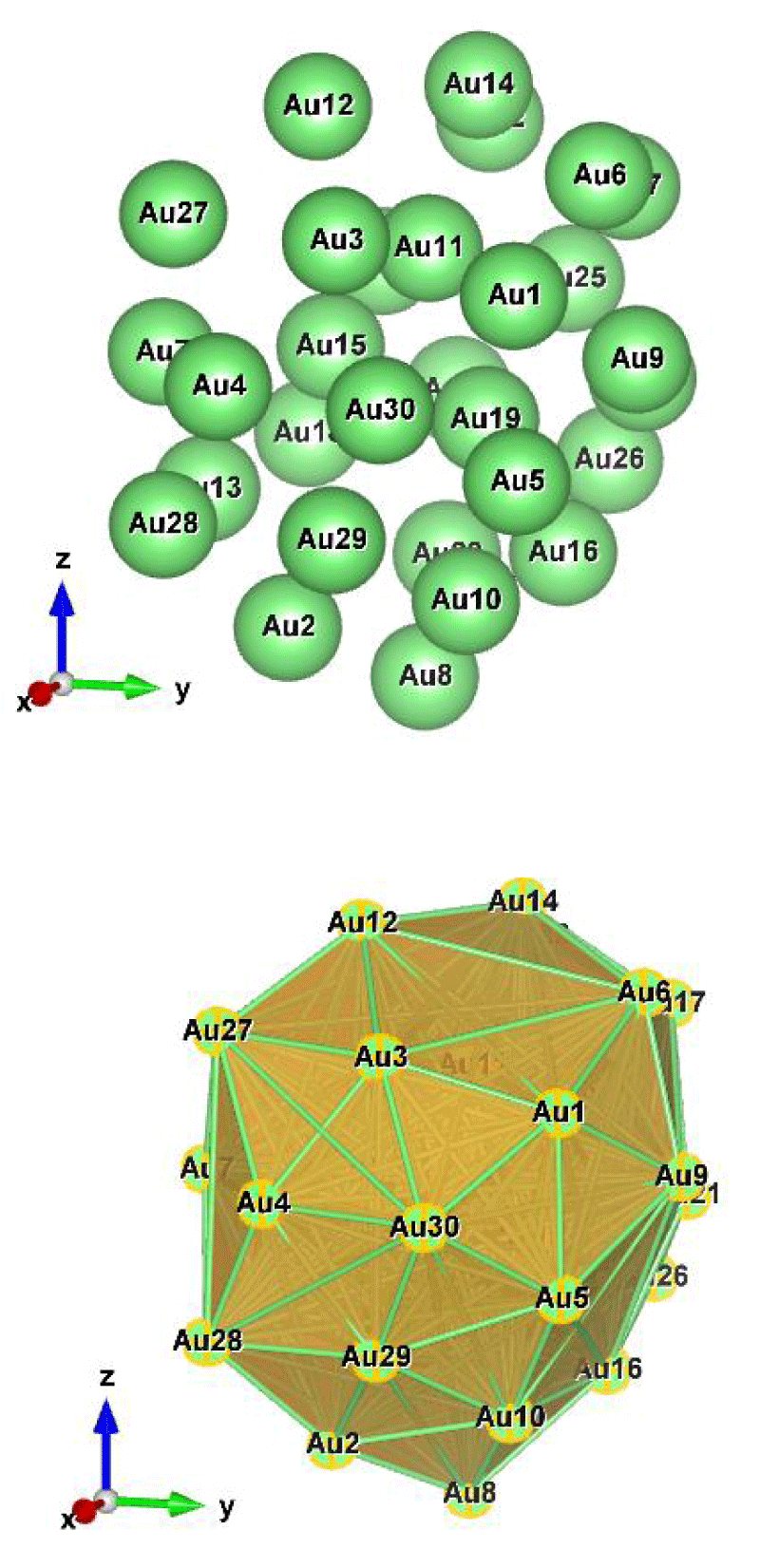
Figure 1: Au26 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au26 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 6.58-9.39 cm−1, which is only for the very first 3 NVM that comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 4-58 NVM, the frequency ranges have occurred between 10.70-197.37 cm−1, which comes within the range of Far Infrared FIR, IR-C 200- 10 cm−1. Thirdly, the rest of the 59-72 NVM, is having the maximum high frequencies, which are ((ωi) - 202.15-319.61 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{23.38, 23.71}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Certainly, such kind of spectrum could be highly possible to observe in the experimental calculations. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
Very recently, Fa, Wei, and Jin-ming Dong [29] have shown the VDOS and corresponding FIR absorption spectrum of the lowest-energy tube-like Au26. Yes, the vibration density of states (VDOS) was obtained by a convolution with a Lorentzian broadening of 2 cm-1. They have shown in Figure 2, the normal frequencies of the tube-like D6dAu26 locate in the range of 23-185 cm-1. Only a portion of its vibration modes are infrared-active due to its high symmetry, and as a result, its far-infrared (FIR) spectrum exhibits some well-resolved peaks. They have had a hope that the infrared resonance-enhanced multiple photon dissociation measurements can be used to acquire the FIR absorption spectrum of Au26, as those done for vanadium and niobium clusters [64-66], so that the existence of their tube-like D6dAu26 can be validated. In addition, they also noticed that the tube-like D6dAu26 has a radial breathing-like mode at 119 cm-1, characteristic of the tube-like or cage structures, which is similar to radial breaking modes found in the carbon nanotubes, and so may be tested by future Raman spectra. Our calculated spectral range (refer to Tables 1-10) is in excellent agreement with theoretical and experimental predictions [29].
For larger sizes of n = 26-30, pyramidal motifs tend to dominate the lower-lying population rather than tubular conformations as previously reported. The energy gaps, excitation energies, and exciton binding energies were also computed to test out the performance of the computational methods employed. Accordingly, a density functional with long-range exchange effects was highly recommended to quantitatively investigate both the ground and excited states of pure gold clusters [67].
The vibrational frequency (ωi) range of the cluster Au27 at ∆E = 0
Table 2 shows the low (at the least) and the high (at the most) frequency range of the cluster Au27, which occurs between 9.44 and 314.57 cm−1, and the lowest energy geometrical structural view can be seen in Figure 2.
| Table 2: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au27 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 9.44 | 34 | 83.22 | 67 | 252.37 |
| 2 | 12.06 | 35 | 83.81 | 68 | 262.49 |
| 3 | 13.02 | 36 | 87.41 | 69 | 268.77 |
| 4 | 15.04 | 37 | 90.60 | 70 | 269.62 |
| 5 | 15.67 | 38 | 94.95 | 71 | 277.72 |
| 6 | 17.84 | 39 | 103.39 | 72 | 279.89 |
| 7 | 18.03 | 40 | 109.89 | 73 | 293.66 |
| 8 | 20.13 | 41 | 112.30 | 74 | 305.85 |
| 9 | 22.31 | 42 | 115.90 | 75 | 314.57 |
| 10 | 22.92 | 43 | 122.58 | 76 | - |
| 11 | 24.14 | 44 | 122.99 | 77 | - |
| 12 | 26.28 | 45 | 130.27 | 78 | - |
| 13 | 29.30 | 46 | 137.14 | 79 | - |
| 14 | 31.97 | 47 | 139.33 | 80 | - |
| 15 | 33.17 | 48 | 143.43 | 81 | - |
| 16 | 33.90 | 49 | 149.53 | 82 | - |
| 17 | 35.55 | 50 | 154.29 | 83 | - |
| 18 | 38.46 | 51 | 162.43 | 84 | - |
| 19 | 41.32 | 52 | 166.29 | 85 | - |
| 20 | 43.93 | 53 | 168.51 | 86 | - |
| 21 | 46.82 | 54 | 175.58 | 87 | - |
| 22 | 50.96 | 55 | 178.73 | 88 | - |
| 23 | 51.42 | 56 | 183.78 | 89 | - |
| 24 | 55.47 | 57 | 190.90 | 90 | - |
| 25 | 57.71 | 58 | 197.47 | 91 | - |
| 26 | 58.50 | 59 | 199.84 | 92 | - |
| 27 | 60.57 | 60 | 203.97 | 93 | - |
| 28 | 62.89 | 61 | 208.28 | 94 | - |
| 29 | 67.39 | 62 | 211.58 | 95 | - |
| 30 | 69.84 | 63 | 214.54 | 96 | - |
| 31 | 71.58 | 64 | 230.78 | 97 | - |
| 32 | 76.29 | 65 | 237.12 | 98 | - |
| 33 | 80.66 | 66 | 248.82 | 99 | - |
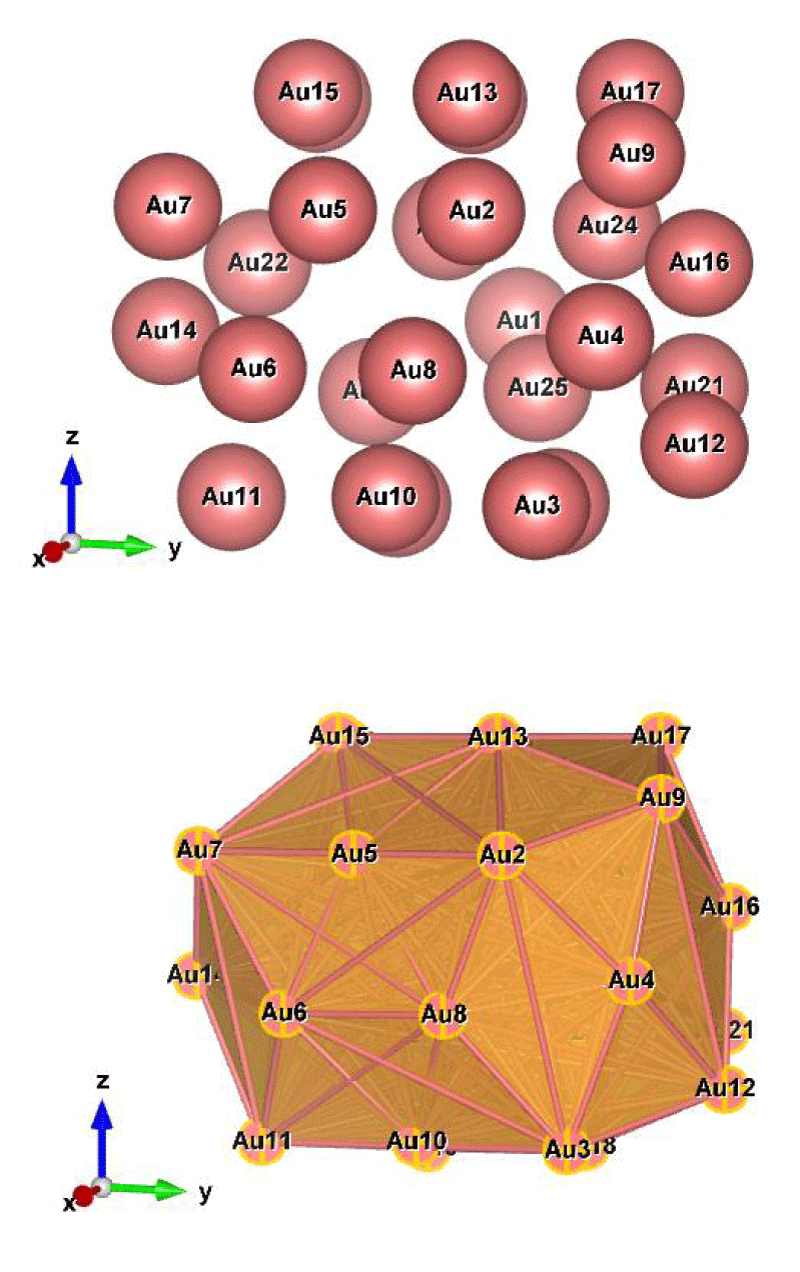
Figure 2: Au27 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au27 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has only one low frequency (ωmin) 9.44 cm−1, which is only for the very first NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 2-59 NVM, the frequency ranges have occurred between 12.06-199.84 cm−1, which comes within the range of Far Infrared FIR, IR-C 200- 10 cm−1. Thirdly, the rest of the 60-75 NVM, is having the maximum high frequencies, which are ((ωi) - 203.97-314.57 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{15.04, 15.67}; {22.31, 22.92}; {33.17, 33.90}; {83.22, 83.81} and {122.58, 122.99}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Certainly, such kind of spectrum could be highly possible to observe in the experimental calculations. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
Nhat PV, et al. have shown that many Au27 isomers were predicted to be energetically quasi-degenerate, the corresponding distinctive vibrational signatures could be used as fingerprints for the identification of cluster geometrical features [68].
New photoelectron spectroscopy (PES) data were obtained using Ar-seeded He supersonic beams to achieve better cluster cooling, resulting in well-resolved spectra and revealing the presence of low-lying isomers in a number of systems. Density-functional theory calculations were used for global minimum searches. For each cluster anion, more than 200 low-lying isomers are generated using the basin-hopping global minimum search algorithm. The most viable structures and low-lying isomers were obtained using both the relative energies and comparisons between the simulated spectra and experimental PES data [28].
The global minimum structures of Aun- (n = 27, 28, 30, and 32-35) are found to exhibit low-symmetry core-shell structures with the number of core atoms increasing with cluster size: Au27-, Au28-, and Au30- possess a one-atom core; Au32- features a three-atom triangular core, and Au33- to Au35- all contain a four-atom tetrahedral core. The global searches reveal that the tetrahedral core is a popular motif for low-lying structures of Au33- to Au35-. The structural information forms the basis for future chemisorption studies to unravel the catalytic effects of gold nanoparticles [28].
The vibrational frequency (ωi) range of the cluster Au28 at ∆E = 0
Table 3 shows the low (at the least) and the high (at the most) frequency range of the cluster Au28, which occurs between 3.44 and 347.32 cm−1, and the lowest energy geometrical structural view can be seen in Figure 3.
| Table 3: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au28 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 3.44 | 34 | 71.90 | 67 | 223.32 |
| 2 | 5.97 | 35 | 74.57 | 68 | 224.94 |
| 3 | 8.54 | 36 | 75.35 | 69 | 234.57 |
| 4 | 10.69 | 37 | 80.47 | 70 | 245.19 |
| 5 | 11.19 | 38 | 82.57 | 71 | 248.60 |
| 6 | 11.41 | 39 | 89.17 | 72 | 261.29 |
| 7 | 13.34 | 40 | 94.30 | 73 | 265.51 |
| 8 | 14.74 | 41 | 96.39 | 74 | 276.00 |
| 9 | 16.02 | 42 | 101.25 | 75 | 285.42 |
| 10 | 17.35 | 43 | 103.42 | 76 | 300.57 |
| 11 | 18.26 | 44 | 109.54 | 77 | 336.31 |
| 12 | 22.09 | 45 | 113.33 | 78 | 347.32 |
| 13 | 23.20 | 46 | 117.44 | 79 | - |
| 14 | 23.72 | 47 | 119.48 | 80 | - |
| 15 | 26.59 | 48 | 121.17 | 81 | - |
| 16 | 27.73 | 49 | 127.25 | 82 | - |
| 17 | 30.21 | 50 | 131.03 | 83 | - |
| 18 | 30.69 | 51 | 137.09 | 84 | - |
| 19 | 33.85 | 52 | 142.67 | 85 | - |
| 20 | 35.23 | 53 | 148.05 | 86 | - |
| 21 | 37.24 | 54 | 150.42 | 87 | - |
| 22 | 39.26 | 55 | 153.40 | 88 | - |
| 23 | 40.33 | 56 | 164.08 | 89 | - |
| 24 | 43.62 | 57 | 172.26 | 90 | - |
| 25 | 45.31 | 58 | 172.82 | 91 | - |
| 26 | 49.10 | 59 | 177.05 | 92 | - |
| 27 | 50.90 | 60 | 177.14 | 93 | - |
| 28 | 55.10 | 61 | 190.90 | 94 | - |
| 29 | 57.50 | 62 | 195.49 | 95 | - |
| 30 | 58.48 | 63 | 202.34 | 96 | - |
| 31 | 61.40 | 64 | 207.69 | 97 | - |
| 32 | 64.27 | 65 | 213.68 | 98 | - |
| 33 | 67.89 | 66 | 218.24 | 99 | - |
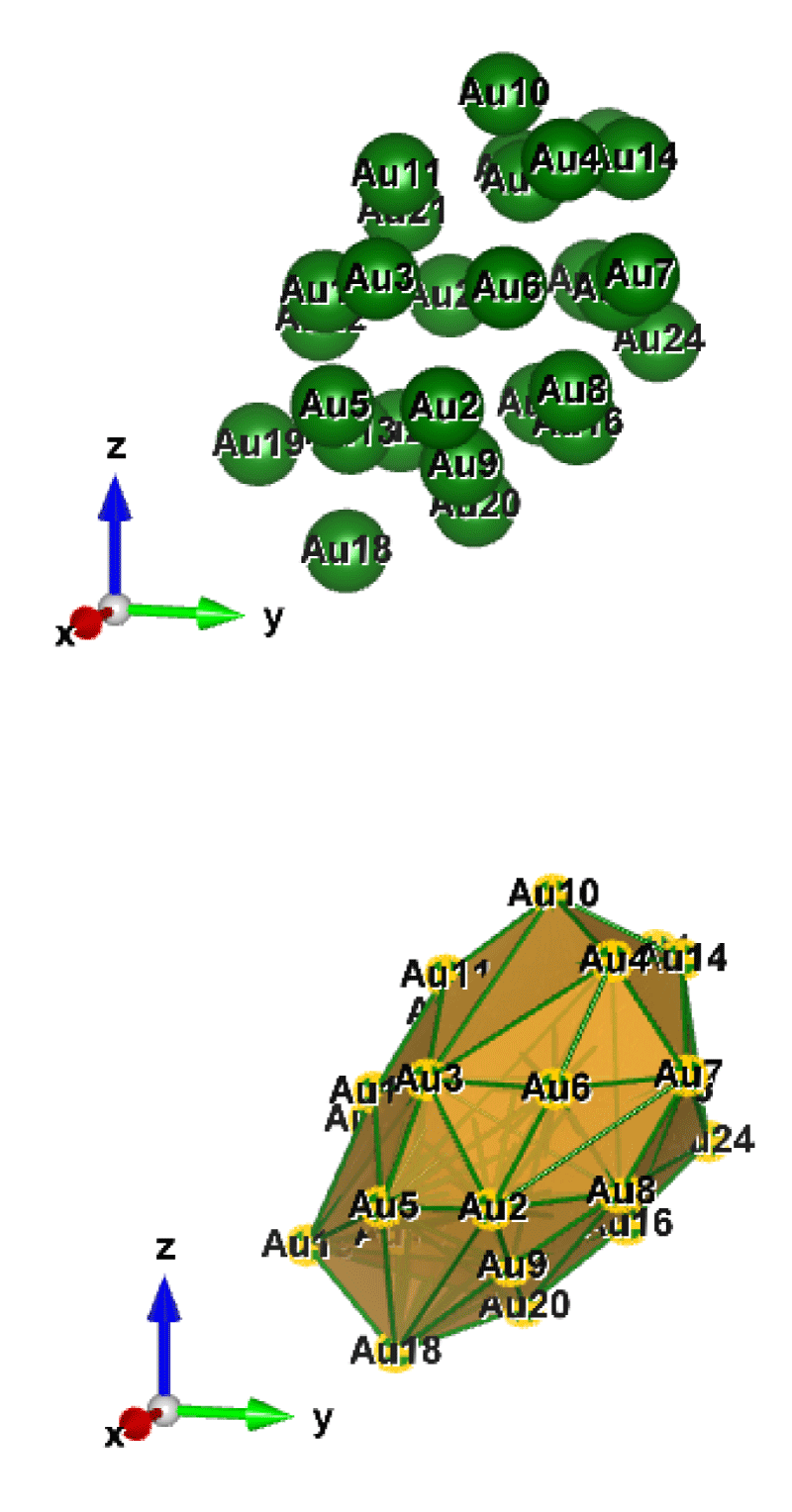
Figure 3: Au28 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au28 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 3.44 - 8.54 cm−1, which is only for the very first 3 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200 - 10 cm−1. Secondly, for the 4-62 NVM, the frequency ranges occurred between 10.69-195.49 cm−1 which comes within the range of Far Infrared FIR, IR-C 200 - 10 cm−1. Thirdly, the rest of the 63-78 NVM, is having the maximum high frequencies, which are ((ωi) - 202.34-347.32 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330 - 200 cm−1.
The double state degeneracy, ωi: [{11.19, 11.41}; {23.20, 23.72}; {30.21, 30.69}; {172.26, 172.82} and {177.05, 177.14}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the two different elliptical motions but that could be a single motion as an individual.
The global minimum structures of Aun-(n = 27, 28, 30, and 32-35) are found to exhibit low-symmetry core-shell structures with the number of core atoms increasing with cluster size: Au27-, Au28-, and Au30- possess a one-atom core; Au32- features a three-atom triangular core, and Au33- to Au35- all contain a four-atom tetrahedral core. The global searches reveal that the tetrahedral core is a popular motif for low-lying structures of Au33- to Au35-. The structural information forms the basis for future chemisorption studies to unravel the catalytic effects of gold nanoparticles [28].
Applications: The recently reported crystal structure of the Au28(TBBT)20 cluster (TBBT: p-test-butylbenzenethiolate) was analyzed with (time-dependent) density functional theory (TD-DFT). Bader charge analysis reveals a novel trimeric Au3(SR)4 binding motif. The cluster can be formulated as Au14((SR)3)4(Au3(SR)4)2. The electronic structure of the Au146+ core and the ligand-protected cluster were analyzed, and their stability could be explained by the formation of distorted eight-electron superatoms. Optical absorption and circular dichroism (CD) spectra were calculated and compared to the experiment. Assignment of handedness of the intrinsically chiral cluster is possible [69].
Wang, Shuxin, et al. substituted gold atoms in fcc-structured Au28 and Au36 nanoclusters with Ag(I)SR complex and obtained AgxAu28-x and AgxAu36-x nanoclusters, respectively [70]. Lin Xiong, et al. proposed a novel ‘gold-atom insertion, thiolate-group elimination’ mechanism to understand the structural evolution of the face-centered-cubic (fcc) thiolate-protected gold clusters. The key step of structural evolution from Au28(SR)20 to Au29(SR)19 and then to the Au30(SR)18 cluster, i.e. the growth of triangle-Au3 units in the gold cores, is understood from the first insertion of an exterior Au(0) atom into the ligand shell and then cleavage of μ2-SR groups [71].
The vibrational frequency (ωi) range of the cluster Au29 at ∆E = 0
Table 4 shows the low (at the least) and the high (at the most) frequency range of the cluster Au29, which occurs between 2.34 and 315.87 cm−1, and the lowest energy geometrical structural view can be seen in Figure 4.
| Table 4: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au29 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 2.34 | 34 | 58.62 | 67 | 200.41 |
| 2 | 7.17 | 35 | 63.19 | 68 | 204.60 |
| 3 | 8.77 | 36 | 64.30 | 69 | 209.86 |
| 4 | 9.74 | 37 | 66.58 | 70 | 216.89 |
| 5 | 10.61 | 38 | 69.46 | 71 | 219.69 |
| 6 | 12.31 | 39 | 75.90 | 72 | 229.33 |
| 7 | 12.95 | 40 | 79.01 | 73 | 232.74 |
| 8 | 13.57 | 41 | 80.65 | 74 | 234.88 |
| 9 | 15.55 | 42 | 81.66 | 75 | 256.95 |
| 10 | 16.83 | 43 | 83.94 | 76 | 260.46 |
| 11 | 18.10 | 44 | 90.55 | 77 | 271.39 |
| 12 | 20.26 | 45 | 94.55 | 78 | 276.27 |
| 13 | 22.51 | 46 | 99.38 | 79 | 290.94 |
| 14 | 25.72 | 47 | 101.05 | 80 | 309.20 |
| 15 | 26.12 | 48 | 105.21 | 81 | 315.87 |
| 16 | 28.37 | 49 | 109.42 | 82 | - |
| 17 | 30.33 | 50 | 110.81 | 83 | - |
| 18 | 31.33 | 51 | 115.14 | 84 | - |
| 19 | 32.49 | 52 | 115.67 | 85 | - |
| 20 | 32.91 | 53 | 122.96 | 86 | - |
| 21 | 35.43 | 54 | 125.73 | 87 | - |
| 22 | 36.89 | 55 | 127.15 | 88 | - |
| 23 | 38.12 | 56 | 133.96 | 89 | - |
| 24 | 39.02 | 57 | 140.95 | 90 | - |
| 25 | 40.44 | 58 | 143.66 | 91 | - |
| 26 | 43.84 | 59 | 147.50 | 92 | - |
| 27 | 44.76 | 60 | 150.01 | 93 | - |
| 28 | 46.73 | 61 | 154.13 | 94 | - |
| 29 | 48.18 | 62 | 159.19 | 95 | - |
| 30 | 49.86 | 63 | 173.21 | 96 | - |
| 31 | 50.97 | 64 | 180.20 | 97 | - |
| 32 | 54.91 | 65 | 183.92 | 98 | - |
| 33 | 56.74 | 66 | 197.10 | 99 | - |
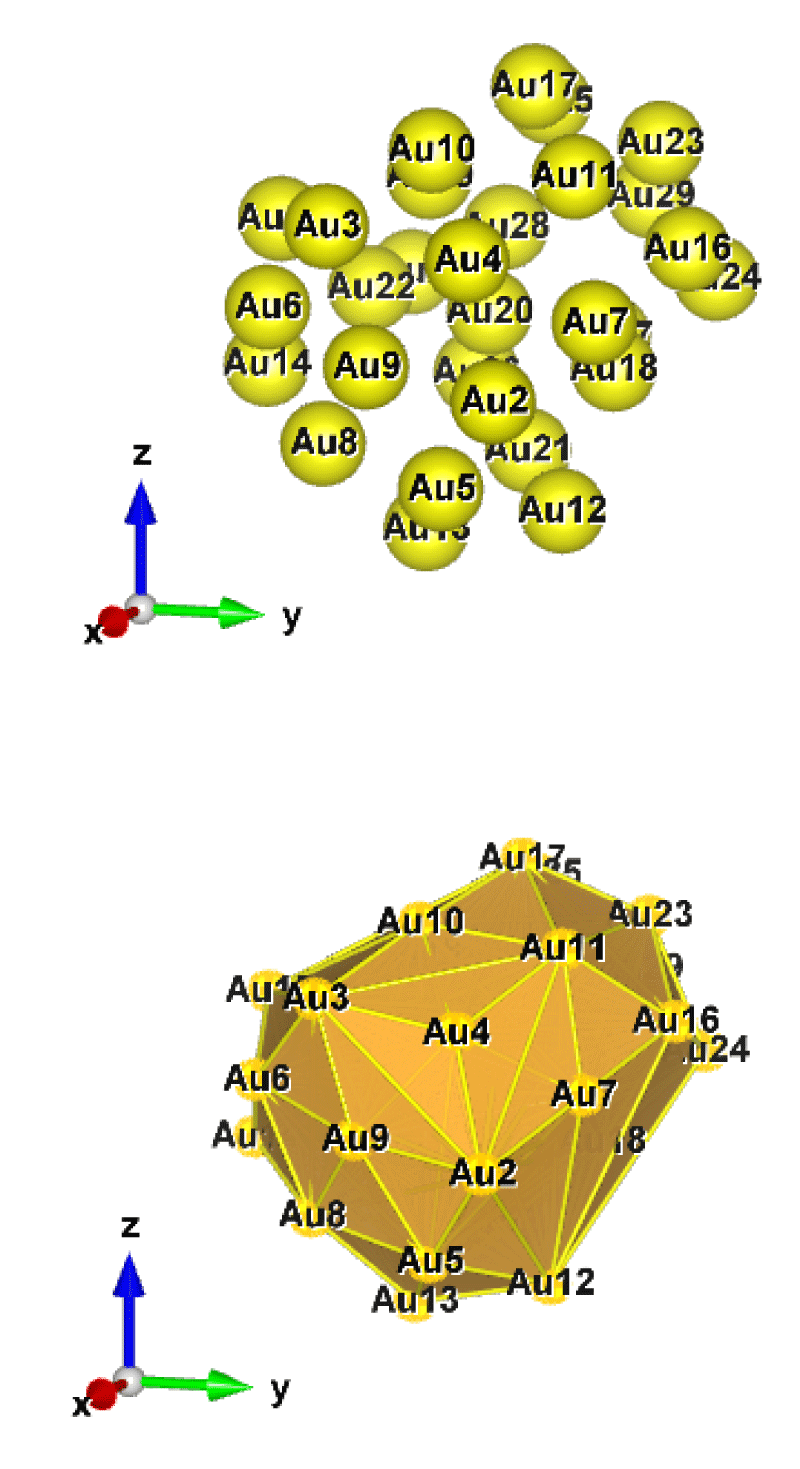
Figure 4: Au29 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au29 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 2.34-9.74 cm−1, which is only for the very first 4 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 5-66 NVM, the frequency ranges occurred between 10.61-197.10 cm−1 which comes within the range of Far Infrared FIR, IR-C 200- 10 cm−1. Thirdly, the rest of the 67-81 NVM, is having the maximum high frequencies, which are ((ωi) - 200.41-315.87 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{12.31, 12.95}; {32.49, 32.91} and {115.14, 115.67}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations, except the first pair can be in silent mode. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
Applications: The atomic structure of a ten-electron (10e) thiolate-protected gold cluster, denoted as Au29(SR)19, was theoretically predicted. Based on the prediction of the atomic structure of the 10e Au29(SR)19 cluster, Lin Xiong, et al. proposed a novel ‘gold-atom insertion, thiolate-group elimination’ mechanism to understand the structural evolution of the face-centered-cubic (fcc) thiolate-protected gold clusters. The key step of structural evolution from Au28(SR)20 to Au29(SR)19 and then to the Au30(SR)18 cluster, i.e. the growth of triangle-Au3 units in the gold cores, is understood from the first insertion of an exterior Au(0) atom into the ligand shell and then cleavage of μ3-SR groups [71].
The vibrational frequency (ωi) range of the cluster Au30 at ∆E = 0
Table 5 shows the low (at the least) and the high (at the most) frequency ranges of the cluster Au30, which are 2.35 and 308.09 cm−1, and the lowest energy geometrical structural view can be seen in Figure 5.
| Table 5: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au30 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 2.35 | 34 | 62.49 | 67 | 184.57 |
| 2 | 7.12 | 35 | 63.91 | 68 | 194.04 |
| 3 | 9.59 | 36 | 65.16 | 69 | 197.11 |
| 4 | 11.30 | 37 | 71.33 | 70 | 200.82 |
| 5 | 15.19 | 38 | 73.45 | 71 | 206.02 |
| 6 | 15.30 | 39 | 75.64 | 72 | 210.31 |
| 7 | 16.84 | 40 | 79.01 | 73 | 213.54 |
| 8 | 17.32 | 41 | 80.25 | 74 | 216.10 |
| 9 | 19.03 | 42 | 82.19 | 75 | 221.37 |
| 10 | 22.45 | 43 | 86.13 | 76 | 229.18 |
| 11 | 23.33 | 44 | 89.52 | 77 | 235.60 |
| 12 | 23.65 | 45 | 94.13 | 78 | 238.08 |
| 13 | 26.05 | 46 | 96.64 | 79 | 243.49 |
| 14 | 27.40 | 47 | 98.86 | 80 | 245.67 |
| 15 | 28.26 | 48 | 104.04 | 81 | 249.27 |
| 16 | 28.73 | 49 | 109.05 | 82 | 260.68 |
| 17 | 31.56 | 50 | 112.34 | 83 | 261.88 |
| 18 | 33.09 | 51 | 114.20 | 84 | 308.09 |
| 19 | 35.11 | 52 | 118.35 | 85 | - |
| 20 | 37.05 | 53 | 124.72 | 86 | - |
| 21 | 37.41 | 54 | 131.18 | 87 | - |
| 22 | 39.69 | 55 | 132.85 | 88 | - |
| 23 | 41.21 | 56 | 140.38 | 89 | - |
| 24 | 42.88 | 57 | 143.58 | 90 | - |
| 25 | 43.55 | 58 | 147.90 | 91 | - |
| 26 | 45.68 | 59 | 149.98 | 92 | - |
| 27 | 47.59 | 60 | 158.29 | 93 | - |
| 28 | 48.91 | 61 | 161.01 | 94 | - |
| 29 | 52.46 | 62 | 163.96 | 95 | - |
| 30 | 53.71 | 63 | 171.15 | 96 | - |
| 31 | 56.04 | 64 | 172.52 | 97 | - |
| 32 | 57.80 | 65 | 176.91 | 98 | - |
| 33 | 61.16 | 66 | 182.65 | 99 | - |
Figure 5: Au30 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au30 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 2.35-9.59 cm−1, which is only for the very first 3 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 4-69 NVM, the frequency ranges have occurred between 11.30-197.11 cm−1 which comes within the range of Far Infrared FIR, IR-C 200-10 cm−1. Thirdly, the rest of the 70-84 NVM, is having the maximum high frequencies, which are ((ωi) - 200.82-308.09 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{15.19, 15.30}; {23.33, 23.65}; {28.26, 28.73} and {37.05, 37.41}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Certainly, such kind of spectrum could be highly possible to observe in the experimental calculations, except for the first pair. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
Structural evolution and stability pattern of pure neutral gold clusters Aun in the small size range of n = 20-30 are examined using density functional theory (DFT) calculations. The equilibrium geometries are either confirmed or determined, and some new ground state structures are identified [67].
For larger sizes of n = 26-30, pyramidal motifs tend to dominate the lower-lying population rather than tubular conformations as previously reported. The energy gaps, excitation energies, and exciton binding energies were also computed to test out the performance of the computational methods employed. Accordingly, a density functional with long-range exchange effects was highly recommended to quantitatively investigate both the ground and excited states of pure gold clusters [67].
The vibrational frequency (ωi) range of the cluster Au31 at ∆E = 0
Table 6 shows the low (at the least) and the high (at the most) frequency range of the cluster Au31, which occurs between 8.98 and 322.69 cm−1, and the lowest energy geometrical structural view can be seen in Figure 6.
| Table 6: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au31 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 8.98 | 34 | 66.56 | 67 | 191.59 |
| 2 | 11.12 | 35 | 66.77 | 68 | 195.09 |
| 3 | 11.18 | 36 | 70.96 | 69 | 195.92 |
| 4 | 13.26 | 37 | 72.24 | 70 | 204.28 |
| 5 | 14.19 | 38 | 75.16 | 71 | 206.91 |
| 6 | 16.25 | 39 | 80.71 | 72 | 210.89 |
| 7 | 18.51 | 40 | 81.75 | 73 | 215.13 |
| 8 | 19.97 | 41 | 82.84 | 74 | 217.46 |
| 9 | 21.76 | 42 | 84.77 | 75 | 221.26 |
| 10 | 22.38 | 43 | 91.92 | 76 | 225.02 |
| 11 | 23.43 | 44 | 94.11 | 77 | 236.70 |
| 12 | 24.52 | 45 | 97.52 | 78 | 240.50 |
| 13 | 25.70 | 46 | 99.67 | 79 | 246.18 |
| 14 | 27.62 | 47 | 103.65 | 80 | 252.30 |
| 15 | 28.51 | 48 | 106.13 | 81 | 255.31 |
| 16 | 31.70 | 49 | 110.95 | 82 | 263.87 |
| 17 | 32.49 | 50 | 114.51 | 83 | 266.21 |
| 18 | 32.87 | 51 | 116.98 | 84 | 270.82 |
| 19 | 34.40 | 52 | 120.17 | 85 | 288.83 |
| 20 | 36.42 | 53 | 126.07 | 86 | 296.43 |
| 21 | 38.92 | 54 | 129.44 | 87 | 322.69 |
| 22 | 39.55 | 55 | 138.09 | 88 | - |
| 23 | 41.52 | 56 | 142.91 | 89 | - |
| 24 | 43.39 | 57 | 148.02 | 90 | - |
| 25 | 46.62 | 58 | 148.35 | 91 | - |
| 26 | 46.98 | 59 | 159.85 | 92 | - |
| 27 | 51.29 | 60 | 161.99 | 93 | - |
| 28 | 52.42 | 61 | 163.55 | 94 | - |
| 29 | 54.99 | 62 | 167.68 | 95 | - |
| 30 | 55.54 | 63 | 168.97 | 96 | - |
| 31 | 57.30 | 64 | 171.15 | 97 | - |
| 32 | 59.46 | 65 | 177.58 | 98 | - |
| 33 | 61.97 | 66 | 183.57 | 99 | - |
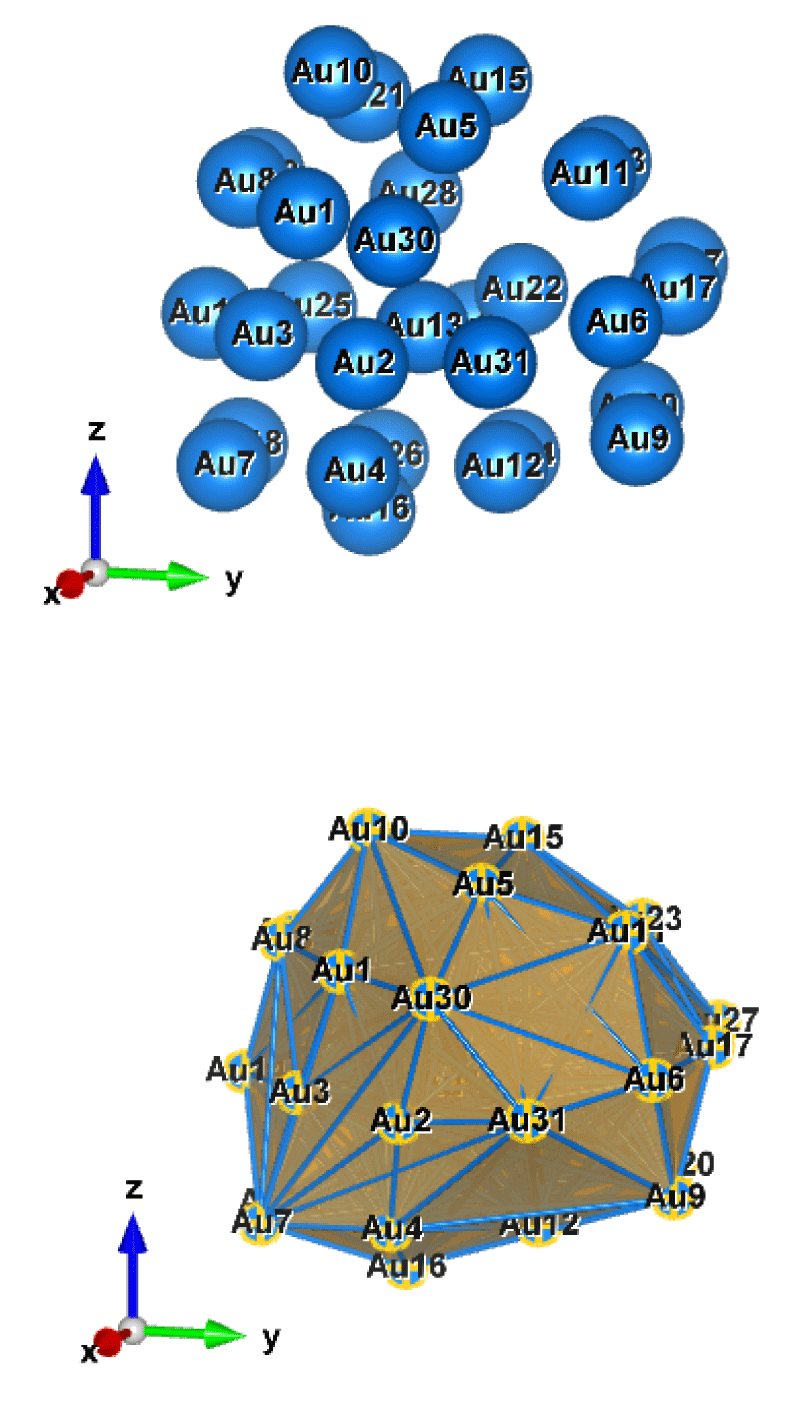
Figure 6: Au31 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au31 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has a low frequency (ωmin) of 8.98 cm−1 which is only for the very first NVM which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 2-69 NVM, the frequency ranges occurred between 11.12-195.72 cm−1 which comes within the range of Far Infrared FIR, IR-C 200-10 cm−1. Thirdly, the rest of the 70-87 NVM, is having the maximum high frequencies, which are ((ωi) - 204.28-322.69 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{11.12, 11.18}; {32.49, 32.87}; {46.62, 46.98}; {66.56, 66.77}; {148.02, 148.35} and {195.09, 195.92}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations, except for the first two pairs that can be in silent modes. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
The structural evolution of negatively charged gold clusters (Aun−) in the medium size range for n = 27-35 has been investigated using photoelectron spectroscopy (PES) and theoretical calculations [28]. Nonetheless, at present, we do not find any literature that compares with our results!
The vibrational frequency (ωi) range of the cluster Au32 at ∆E = 0
Table 7 shows the low (at the least) and the high (at the most) frequency range of the cluster Au32, which occurs between 2.43 and 341.62 cm−1, and the lowest energy geometrical structural view can be seen in Figure 7.
| Table 7: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au32 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 2.43 | 34 | 54.40 | 67 | 164.78 |
| 2 | 5.32 | 35 | 58.71 | 68 | 169.04 |
| 3 | 6.65 | 36 | 60.02 | 69 | 172.13 |
| 4 | 8.07 | 37 | 61.26 | 70 | 174.38 |
| 5 | 10.51 | 38 | 64.86 | 71 | 179.49 |
| 6 | 12.03 | 39 | 66.81 | 72 | 189.59 |
| 7 | 13.63 | 40 | 69.41 | 73 | 192.77 |
| 8 | 14.78 | 41 | 69.79 | 74 | 196.16 |
| 9 | 17.01 | 42 | 70.50 | 75 | 201.19 |
| 10 | 17.54 | 43 | 76.24 | 76 | 208.44 |
| 11 | 19.98 | 44 | 77.65 | 77 | 214.56 |
| 12 | 21.73 | 45 | 80.59 | 78 | 215.82 |
| 13 | 23.01 | 46 | 82.74 | 79 | 217.55 |
| 14 | 23.77 | 47 | 84.60 | 80 | 222.58 |
| 15 | 24.16 | 48 | 86.68 | 81 | 226.53 |
| 16 | 25.51 | 49 | 89.34 | 82 | 236.59 |
| 17 | 27.03 | 50 | 91.93 | 83 | 239.92 |
| 18 | 29.02 | 51 | 95.23 | 84 | 244.35 |
| 19 | 31.37 | 52 | 101.36 | 85 | 247.90 |
| 20 | 32.43 | 53 | 104.59 | 86 | 254.41 |
| 21 | 33.29 | 54 | 105.93 | 87 | 269.72 |
| 22 | 34.83 | 55 | 111.54 | 88 | 284.47 |
| 23 | 36.10 | 56 | 114.46 | 89 | 293.94 |
| 24 | 37.10 | 57 | 115.17 | 90 | 341.62 |
| 25 | 38.54 | 58 | 124.16 | 91 | - |
| 26 | 41.59 | 59 | 132.79 | 92 | - |
| 27 | 43.69 | 60 | 136.77 | 93 | - |
| 28 | 45.11 | 61 | 139.20 | 94 | - |
| 29 | 46.73 | 62 | 146.23 | 95 | - |
| 30 | 47.66 | 63 | 147.91 | 96 | - |
| 31 | 49.36 | 64 | 152.56 | 97 | - |
| 32 | 50.93 | 65 | 157.23 | 98 | - |
| 33 | 53.01 | 66 | 164.25 | 99 | - |
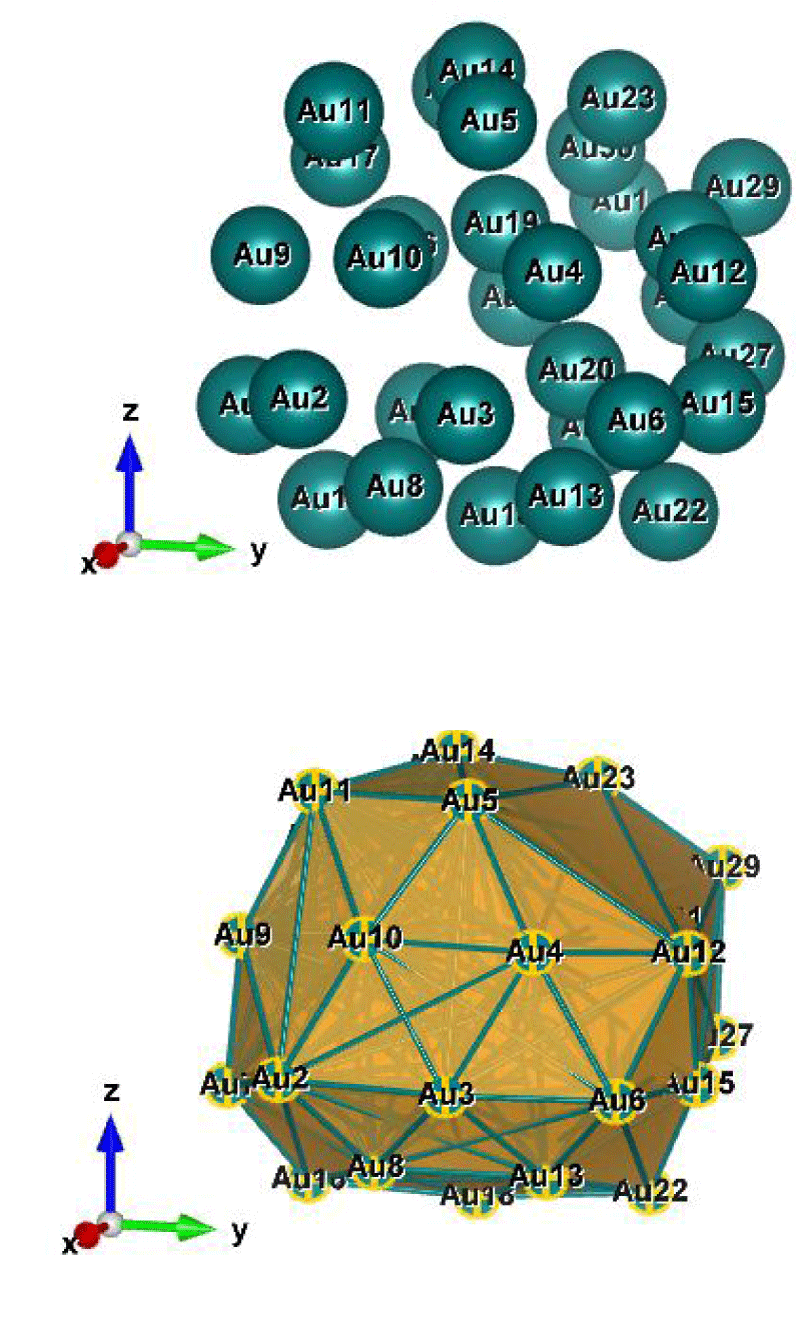
Figure 7: Au32 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au32 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 2.43-8.07 cm−1 which is only for the very first 4 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 5-74 NVM, the frequency ranges occurred between 10.51-196.16 cm−1 which comes within the range of Far Infrared FIR, IR-C 200-10 cm−1. Thirdly, the rest of the 75-90 NVM, is having the maximum high frequencies, which are ((ωi) - 201.19-341.62 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{17.01, 17.54}; {23.01, 23.77}; {69.41, 69.79} and {164.25, 164.78}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations, except the first three pairs can be in a silent mode. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
More recently, a DFT study predicted the existence of the highly stable icosahedron Au32 cage, constructed from the carbon fullerene C60 as a template and so referred to as “golden” fullerene [72,73]. The Au32 fullerene cage satisfies the 2(N+1)2 aromatic rule [74] and has an extremely large energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) up to at least 1.5 eV, showing its chemical stability and its potential ability to assemble into molecular crystals. Furthermore, Gao, et al. and Fa W, et al. have used the BP86 method recently study the Au32 with the DFT relativistic effects and cage-like structure and that was stable chemically and ground state due to the extremely larger bandgap between the HOMO and the LUMO that was approximately up to the 1.7 eV [75,76].
Firstly, for the Gold cluster Au32 in which the numbers of atoms are 32 and it represents the mode at 122.339 cm−1 with the IR Intensity 1.3387 km/mol. Secondly, for the Gold cluster Au32 in which the numbers of atoms are 32 and it represents two modes at the 134.70 cm−1 and 1.2958 cm−1 with the Partial IR Intensity 1.3387 km/mol and 0.003585 km/mol respectively [30].
Although we are not able to compare our results directly with Tahir Iqbal, et al., (The IR Intensity spectra for the gold cluster calculated via DFTB), but possible to compare with the highest amplitude of Aun(n = 32) that is closely matched with our NVM 58, 59, 60 that and the corresponding observed vibrational spectra’s are 124.16 cm−1, 132.79 and 136.77 cm−1 respectively, which is a very good agreement with their results, having the reason with respect to our theoretical setup [30].
Ji, et al. first reported that Au32- is a core-shell cluster with a three-atom triangular core. Further first-principals calculations suggested that the global minimum of Au32- contains a four-atom tetrahedral core [31]. Certainly, neutral Au32 was reported to possess an icosahedral cage structure, a combined DFT and PES study showed that the Au32- cluster anion possesses a more compact core-shell-type structure. Subsequent theoretical calculations support this conclusion [28].
In total, DFT calculations were carried out on bare Au32 and Au33 nanoclusters with various charges, in order to analyze their stability with respect to different cluster electron numbers. Results indicated that in addition to the neutral Au32 hollow species, significant HOMO-LUMO gaps were computed for [Au32]8+ (hollow) and [Au32]4+ (two-shell structure). Species with smaller HOMO-LUMO gaps can reach stability upon “passivation” by a ligand shell, as experimentally exemplified. Icosahedral frameworks of Ih or lower symmetry are favored for the cationic nanoclusters whereas different structures are computed for the anionic ones [26].
The vibrational frequency (ωi) range of the cluster Au33 at ∆E = 0
Table 8 shows the low (at the least) and the high (at the most) frequency range of the cluster Au33, which occurs between 5.49 and 284.91 cm−1, and the lowest energy geometrical structural view can be seen in Figure 8.
| Table 8: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au33 at ΔE = 0. | |||||
| NVM 3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 5.49 | 34 | 59.26 | 67 | 175.57 |
| 2 | 5.79 | 35 | 60.36 | 68 | 176.52 |
| 3 | 7.86 | 36 | 62.09 | 69 | 177.82 |
| 4 | 12.13 | 37 | 64.36 | 70 | 192.00 |
| 5 | 13.71 | 38 | 64.58 | 71 | 192.37 |
| 6 | 15.46 | 39 | 66.77 | 72 | 201.44 |
| 7 | 16.61 | 40 | 72.24 | 73 | 207.91 |
| 8 | 17.23 | 41 | 72.58 | 74 | 216.03 |
| 9 | 17.39 | 42 | 75.87 | 75 | 216.91 |
| 10 | 20.96 | 43 | 76.48 | 76 | 221.56 |
| 11 | 21.37 | 44 | 85.68 | 77 | 221.91 |
| 12 | 22.02 | 45 | 87.70 | 78 | 222.20 |
| 13 | 23.83 | 46 | 94.32 | 79 | 235.78 |
| 14 | 24.33 | 47 | 95.52 | 80 | 237.35 |
| 15 | 24.74 | 48 | 96.22 | 81 | 240.10 |
| 16 | 25.16 | 49 | 100.89 | 82 | 240.86 |
| 17 | 25.75 | 50 | 101.17 | 83 | 241.52 |
| 18 | 26.79 | 51 | 110.61 | 84 | 249.37 |
| 19 | 27.75 | 52 | 111.12 | 85 | 250.62 |
| 20 | 27.94 | 53 | 112.08 | 86 | 252.65 |
| 21 | 29.45 | 54 | 116.55 | 87 | 261.02 |
| 22 | 30.08 | 55 | 117.16 | 88 | 261.80 |
| 23 | 30.70 | 56 | 127.62 | 89 | 266.83 |
| 24 | 31.34 | 57 | 140.31 | 90 | 270.59 |
| 25 | 33.06 | 58 | 141.84 | 91 | 273.37 |
| 26 | 34.09 | 59 | 142.33 | 92 | 284.36 |
| 27 | 36.38 | 60 | 145.48 | 93 | 284.91 |
| 28 | 37.96 | 61 | 147.97 | 94 | - |
| 29 | 45.91 | 62 | 151.88 | 95 | - |
| 30 | 46.80 | 63 | 152.00 | 96 | - |
| 31 | 47.08 | 64 | 158.56 | 97 | - |
| 32 | 54.45 | 65 | 159.32 | 98 | - |
| 33 | 58.84 | 66 | 163.22 | 99 | - |
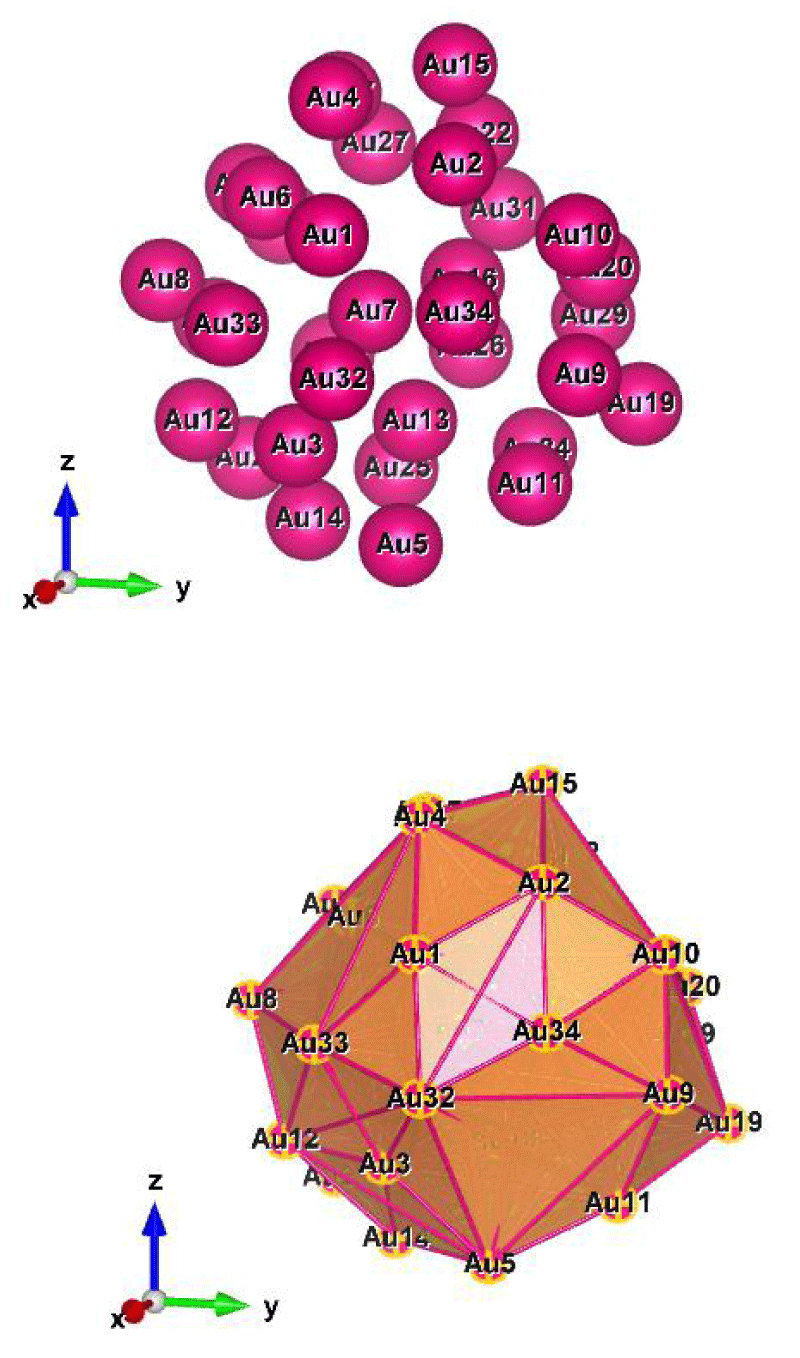
Figure 8: Au33 (D2); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au33 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 5.49-7.86 cm−1 which is only for the very first 3 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 4-71 NVM, the frequency ranges occurred between 12.13-192.37 cm−1 which comes within the range of Far Infrared FIR, IR-C 200- 10 cm−1. Thirdly, the rest of the 72-93 NVM, is having the maximum high frequencies, which are ((ωi) - 201.44-284.91 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{5.49, 5.79}; {17.23, 17.39}; {24.33 24.74}; {25.16, 25.75}; {27.75, 27.94}; {30.08, 30.70}; {64.36, 64.58}; {72.24; 72.58}; {192.00, 192.37}; {216.03, 216.91}; {221.56, 221.91}; {240.10, 240.86}; {261.02, 261.80} and {284.36, 284.91}] in cm−1. The degree of degeneracy has occurred below, as well as within the range of Far Infrared FIR, IR-C 200-10 cm−1 and also falling within the range of Mid Infrared MIR, IR-C 3330-200 cm-1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations, except the first two pairs can be in a silent mode. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
A Special Structure of Au33 (D2): The excellencies of these clusters are having much and full of double-state degeneracy, apart from this, cluster Au33 has many interesting futures; one is, the spectral pair begins at the first two NVM [1,2] itself, as well as, it ends with the extreme last two NVM [92,93], and the second one is, some of the pairs have degenerated consecutively (that will help for rapid degenerate rearrangements of a chemical species), in addition to that, 30.10% spectral covered fully with double pairs in the same level and are all equally probable of being filled, and the rest of them are having single degenerate states, and also the presence of some symmetry in the system, additionally the radial distances of the interatomic distances also plays a major role. Interesting things to be noticed, having 5d and 6s valance electrons per gold atom, the nuclei were smeared out of a spherical medium (jellium), with a constant density inside, which the valence electrons were moving.
The results of DFT calculations by Gu, et al. [36,73] on Aun Clusters with 32 ≤ N ≤ 35 point to the existence of cage-like structures. Fa, et al. [76] suggested that the possible occurrences of the structures related to either fragment of the crystal or to tube-like structures. These tube-like Aun with larger surface area and hollow inner space may be important for fundamental chemistry researches, and in the future, have a wide range of applications in catalysis, biology, nanotechnology, etc.
The orbitals have much lower degeneracy in the DFTB calculations leading to many more, different orbital energies. A very remarkable exception is n = 33 which has only a few different orbital energies and, in addition, is particularly stable. Moreover, we predict that the cluster for n = 33 is particularly stable and symmetric, the reason could be, such kind of clusters often possess their atoms on the surface of the compact core that is bonded (for covalently bonded elements, the effects due to directional bonds are dominating) to only one or two nearest neighbors, that is one of the main reasons, that our re-optimized structures do not have a very high symmetry (when including orbital interactions). Most significantly, lower nuclear charge effects on the neighboring electrons drive the greater change of electron density that causes the rise of the bond distance due to vibration stimulation and these changes in vibrations are the fundamental interest in Raman spectroscopy. Various experimental studies are reported for molecular scale in the literature that exploits the optical spectra, high polarizability, and emission properties of the noble metal clusters [77 - 80].
Supporting Information: It is all shown through two different types of structural views: The first one is, a view along the a, b, and c-axis and also a view along the *, b*, and c* axis (Figures 8 (a-f)). The second one is, to rotate around the x-axis (upward direction) and to rotate around the x-axis (downward direction); to rotate around the y-axis (right side direction) and to rotate around the y-axis (left side direction); to rotate around the z-axis (clockwise direction) and to rotate around the z-axis (anti-clockwise direction) (Figures 8 (A-F)).
Of course, it is interesting to seek other non-space-filled gold clusters as potential true ground states for the bigger sizes. Therefore, further computational efforts are still needed to explore the energy landscapes of these medium-sized gold clusters. Nonetheless, Au33 prefers a highly symmetric tube-like structure without core atoms!
In particular, the figure shows that the Au33 cluster is exceptional and different from the other ones (Please refer, to the Supporting Information and the title of Figures 8 (a-f) and Figures 8 (A-F)).
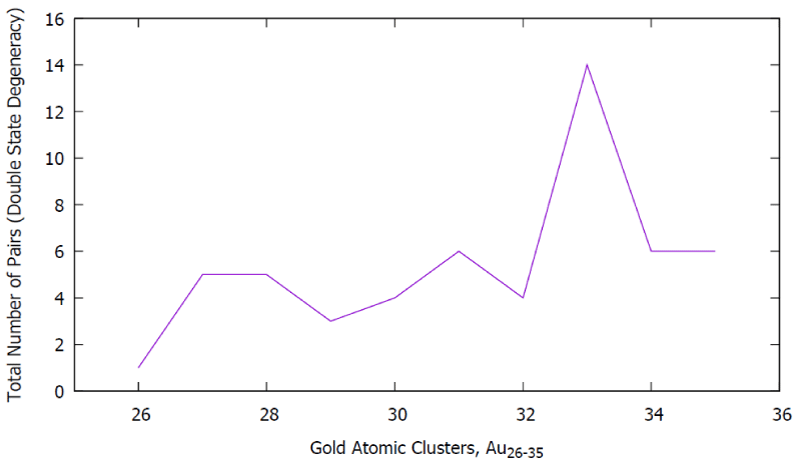
Figure G. Clusters Au26-35 vs. the total number of pairs (the double-state degeneracy).
Figure G: Clusters Au26-35 vs. the total number of pairs (the double-state degeneracy).
The vibrational frequency (ωi) range of the cluster Au34 at ∆E = 0
Table 9 shows the low (at the least) and the high (at the most) frequency range of the cluster Au34, which occurs between 5.06 and 322.42 cm−1, and the lowest energy geometrical structural view can be seen in Figure 9.
| Table 9: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au34 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 5.06 | 34 | 53.66 | 67 | 142.84 |
| 2 | 6.12 | 35 | 56.76 | 68 | 152.88 |
| 3 | 7.54 | 36 | 57.13 | 69 | 156.98 |
| 4 | 8.47 | 37 | 58.61 | 70 | 158.99 |
| 5 | 10.54 | 38 | 62.00 | 71 | 164.54 |
| 6 | 10.78 | 39 | 63.25 | 72 | 169.82 |
| 7 | 13.04 | 40 | 66.12 | 73 | 174.83 |
| 8 | 14.25 | 41 | 67.80 | 74 | 177.84 |
| 9 | 15.33 | 42 | 68.31 | 75 | 184.60 |
| 10 | 16.19 | 43 | 70.21 | 76 | 185.74 |
| 11 | 17.28 | 44 | 73.75 | 77 | 187.84 |
| 12 | 19.44 | 45 | 75.44 | 78 | 192.60 |
| 13 | 19.72 | 46 | 77.38 | 79 | 201.66 |
| 14 | 21.41 | 47 | 81.84 | 80 | 204.09 |
| 15 | 23.41 | 48 | 85.36 | 81 | 207.32 |
| 16 | 26.66 | 49 | 87.24 | 82 | 210.44 |
| 17 | 27.56 | 50 | 91.13 | 83 | 212.87 |
| 18 | 28.69 | 51 | 93.57 | 84 | 220.44 |
| 19 | 30.70 | 52 | 96.47 | 85 | 225.24 |
| 20 | 31.79 | 53 | 96.58 | 86 | 230.25 |
| 21 | 32.80 | 54 | 100.27 | 87 | 232.29 |
| 22 | 34.03 | 55 | 104.18 | 88 | 234.00 |
| 23 | 35.19 | 56 | 107.47 | 89 | 243.87 |
| 24 | 36.08 | 57 | 108.79 | 90 | 244.46 |
| 25 | 38.08 | 58 | 115.11 | 91 | 252.96 |
| 26 | 39.76 | 59 | 115.75 | 92 | 255.44 |
| 27 | 41.61 | 60 | 117.87 | 93 | 265.64 |
| 28 | 42.39 | 61 | 126.48 | 94 | 279.82 |
| 29 | 46.67 | 62 | 129.24 | 95 | 285.13 |
| 30 | 48.23 | 63 | 132.08 | 96 | 322.42 |
| 31 | 49.01 | 64 | 135.07 | 97 | - |
| 32 | 50.11 | 65 | 136.76 | 98 | - |
| 33 | 53.13 | 66 | 142.45 | 99 | - |
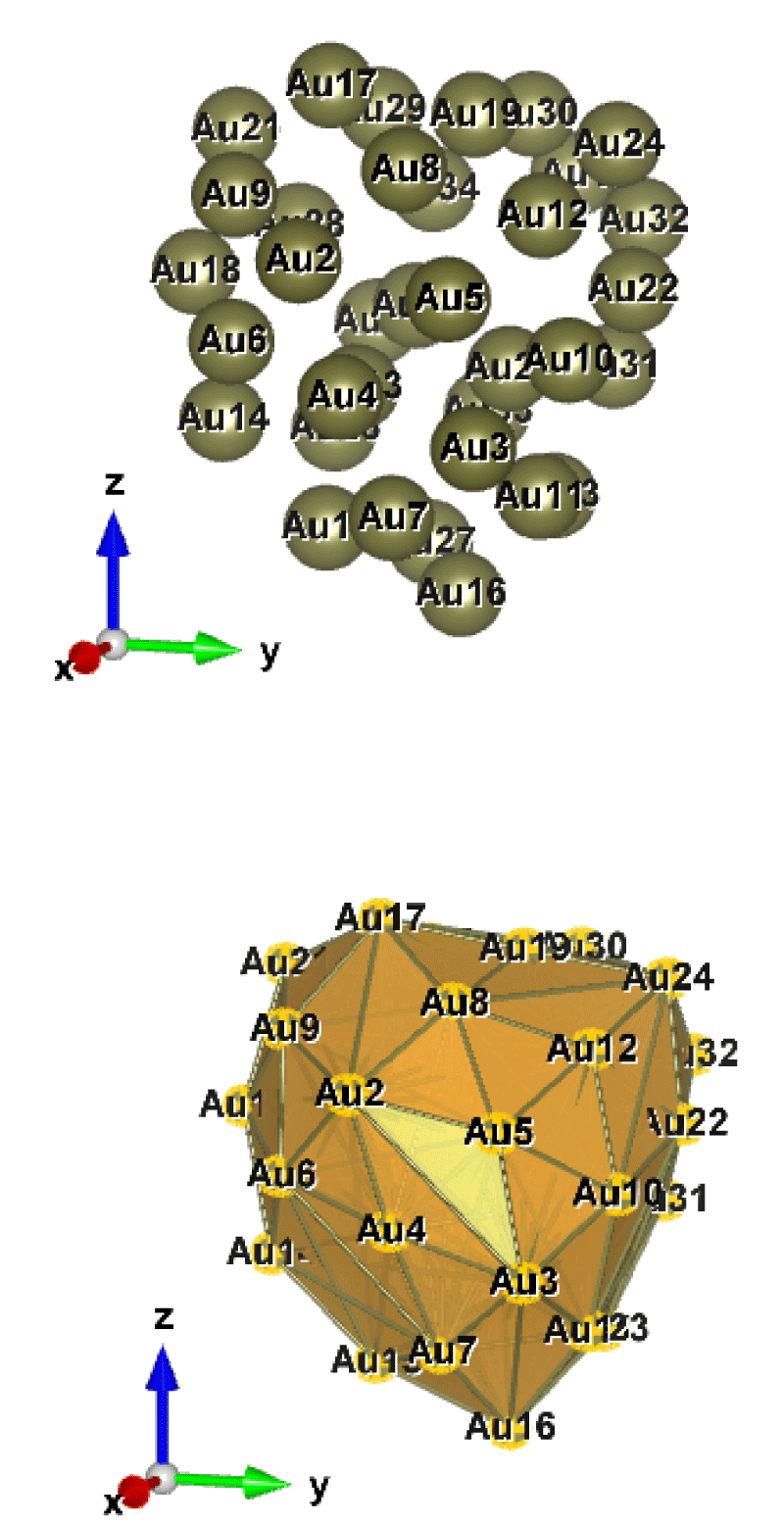
Figure 9: Au34 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structures of the Au34 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 5.06-8.47 cm−1 which is only for the very first 4 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 5-78 NVM, the frequency ranges occurred between 10.54-192.60 cm−1 which comes within the range of Far Infrared FIR, IR-C 200- 10 cm−1. Thirdly, the rest of the 79-96 NVM, is having the maximum high frequencies, which are ((ωi) - 201.66-322.42 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{10.54, 10.78}; {19.44, 19.72}; {53.13, 53.66}; {96.47, 96.58}; {115.11, 115.75} and {142.45, 142.84}] in cm−1. The degree of degeneracy has occurred within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
Xiao Gu, et al. [81], have confirmed that among the large Aun- clusters for n > 20, the photoelectron spectra of Au34- exhibit the largest energy gap (0.94 eV) with well-resolved spectral features, making it a good candidate for structural consideration in conjunction with theoretical studies. Extensive structural searches at several levels of density functional and ab initio theory revealed that the low-lying isomers of Au34- can be characterized as fluxional core-shell type structures with 4 or 3 inner atoms and 30 or 31 outer atoms, i.e., Au4@Au30- and Au3@Au31-, respectively. Detailed comparisons between theoretical and photoelectron results suggest that the most probable ground state structures of Au34- are of the Au4@Au30- type. The 30 outer atoms seem to be disordered or fluxional, giving rise to a number of low-lying isomers with very close energies and simulated photoelectron spectra. The fluxional nature of the outer layer in large gold clusters or nanoparticles may have important implications for their remarkable catalytic activities [81].
Itzel E. Santizo, et al. provided theoretical evidence for the existence of energetically stable chiral structures for bare gold clusters. Density functional theory calculations within the generalized-gradient approximation were performed to systematically study structural, vibrational, electronic, and optical properties of the lowest-lying isomers of the Au34Z, (Z = +1, 0, -1), clusters. Their results show that for the neutral and charged clusters, the lowest-energy isomer has a C1 (chiral) structure. In addition, a C3 (chiral) isomer was found to nearly degenerate in energy with the C1 isomer. Those results are in agreement with previous theoretical-experimental studies done for the Au34- cluster; however, because their calculated molecular scattering functions for the C1 and C3 isomers of this cluster are almost indistinguishable, it is concluded that the actual resolution in trapped ion electron diffraction experiments was not enough to discriminate between them [82].
On the other hand, the electronic density of states of the C1 isomer shows better overall agreement with the measured photoelectron spectrum of the Au34− cluster than that one corresponding to the C3 isomer. The electronic density of states of these isomers also shows different features in the energy region of the HOMO-LUMO gap, which would generate distinct behavior in their optical properties. In fact, the calculated absorption and circular dichroism spectra of the two chiral isomers show clear differences in their line shape. Another important property that distinguishes the C1 and C3 isomers is the different spatial distribution of the atomic coordination on the cluster surface. Our results confirm that the potential energy surface (PES) of bare gold clusters could have the lowest-lying energy minima corresponding to intrinsically chiral structures [82].
In addition to that, the structures of the Au34- cluster have been studied both by TIED and PES, showing that its global minimum also consists of core-shell type structures with a four-atom core. For Au34-, the combined TIED and DFT study resulted in a C3 core-shell cluster with a four-atom tetrahedral core, but the PES and DFT study found two low symmetry (C1) core-shell structures, both with a four-atom tetrahedral core, competing for the global minimum. The low-symmetry C1 structure for Au34- has been confirmed by two subsequent DFT studies [34-37, 81-83].
The vibrational frequency (ωi) range of the cluster Au35 at ∆E = 0
Table 10 shows the low (at the least) and the high (at the most) frequency range of the cluster Au35, which occurs between 2.04 and 300.43 cm−1, and the lowest energy geometrical structural view can be seen in Figure 10.
| Table 10: The Normal modes (NVM) and the vibrational frequencies (ωi) of Au35 at ΔE = 0. | |||||
| NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] | NVM (3N-6) | ωi [cm−1] |
| 1 | 2.04 | 34 | 48.34 | 67 | 136.14 |
| 2 | 3.09 | 35 | 49.18 | 68 | 138.71 |
| 3 | 3.44 | 36 | 50.78 | 69 | 142.55 |
| 4 | 6.06 | 37 | 53.20 | 70 | 145.31 |
| 5 | 9.01 | 38 | 53.49 | 71 | 150.28 |
| 6 | 9.69 | 39 | 57.39 | 72 | 152.88 |
| 7 | 10.08 | 40 | 58.29 | 73 | 160.06 |
| 8 | 11.56 | 41 | 61.94 | 74 | 163.33 |
| 9 | 12.42 | 42 | 65.08 | 75 | 172.18 |
| 10 | 13.40 | 43 | 65.43 | 76 | 173.57 |
| 11 | 14.85 | 44 | 67.21 | 77 | 177.20 |
| 12 | 15.57 | 45 | 69.64 | 78 | 179.07 |
| 13 | 16.93 | 46 | 71.72 | 79 | 182.17 |
| 14 | 17.86 | 47 | 73.88 | 80 | 185.42 |
| 15 | 19.05 | 48 | 76.07 | 81 | 187.81 |
| 16 | 19.83 | 49 | 76.67 | 82 | 191.55 |
| 17 | 20.97 | 50 | 80.58 | 83 | 193.52 |
| 18 | 22.30 | 51 | 81.64 | 84 | 196.65 |
| 19 | 23.86 | 52 | 85.57 | 85 | 201.36 |
| 20 | 24.22 | 53 | 87.49 | 86 | 204.70 |
| 21 | 25.29 | 54 | 90.82 | 87 | 206.87 |
| 22 | 28.19 | 55 | 92.64 | 88 | 211.61 |
| 23 | 29.46 | 56 | 95.39 | 89 | 218.80 |
| 24 | 30.74 | 57 | 98.79 | 90 | 224.10 |
| 25 | 32.01 | 58 | 102.10 | 91 | 229.28 |
| 26 | 35.10 | 59 | 103.18 | 92 | 237.01 |
| 27 | 36.14 | 60 | 107.72 | 93 | 239.16 |
| 28 | 37.75 | 61 | 111.41 | 94 | 243.05 |
| 29 | 40.18 | 62 | 116.18 | 95 | 249.56 |
| 30 | 43.03 | 63 | 120.32 | 96 | 254.40 |
| 31 | 44.19 | 64 | 121.08 | 97 | 255.10 |
| 32 | 45.49 | 65 | 128.81 | 98 | 261.72 |
| 33 | 46.66 | 66 | 132.75 | 99 | 300.43 |
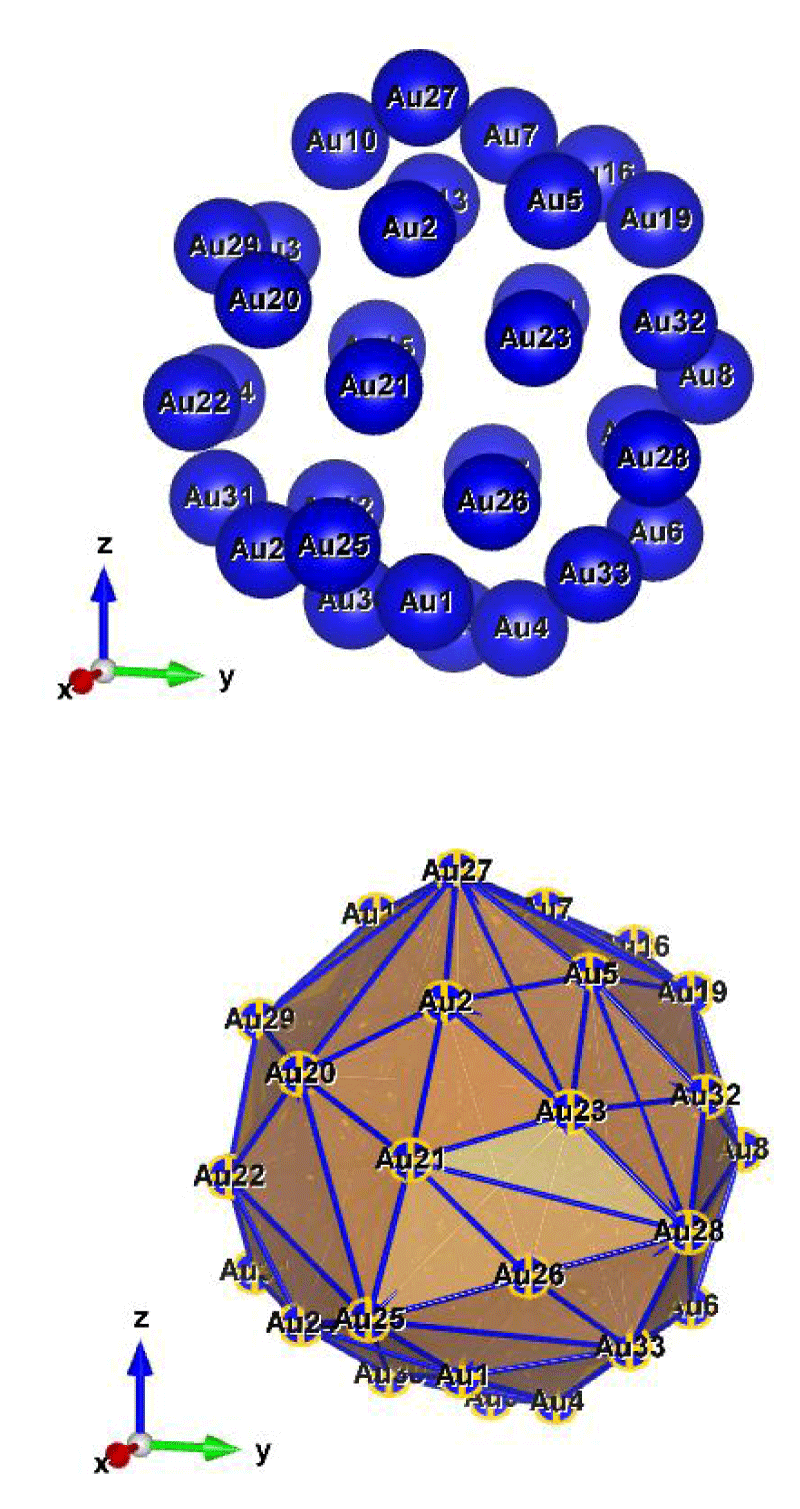
Figure 10: Au35 (C1); Style (Space-filling [top], Polyhedral [bottom]): The lowest energy geometrical structure of the Au35 cluster. Standard orientation of crystal shape at ∆E = 0.
Firstly, the cluster has some low frequencies (ωmin) between 2.04-9.69 cm−1 which is only for the very first 6 NVM, which comes even below the scale of Far Infrared FIR, IR-C 200-10 cm−1. Secondly, for the 7-84 NVM, the frequency ranges occurred between 10.08-196.65 cm−1 which comes within the range of Far Infrared FIR, IR-C 200-10 cm−1. Thirdly, the rest of the 85-99 NVM, is having the maximum high frequencies, which are ((ωi) - 201.36-300.43 cm−1) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm−1.
The double state degeneracy, ωi: [{3.09, 3.44}; {9.01, 9.69}; {19.05, 19.83}; {53.20, 53.49}; {65.08, 65.43} and {76.07, 76.67}] in cm−1. The degree of degeneracy has occurred below, as well as within the range of Far Infrared FIR, IR-C 200-10 cm−1. Surely, such kind of spectrum could be highly possible to observe in the experimental calculations, except the first pair can be in silent modes. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion but that could be a single motion.
The results of DFT calculations by Gu, et al. [36] on Aun Clusters with 32 ≤ N ≤ 35 point to the existence of cage-like structures. Fa, et al. [29] suggested that the possible occurrences of the structures related to either fragments of the crystal or tube-like structures. These tube-like Aun with larger surface area and hollow inner space may be important for fundamental chemistry research and in the future, have a wide range of applications in catalysis, biology, nanotechnology, etc.
The overall shape of the clusters: A spherical shape, a lens-like shape, and a cigar-like shape.
Can we observe the Structural Evolution and Growth Pattern of Mid-sized Gold Atomic Clusters?
From Figures 1-10 (that includes, [Figure 8a)] and [Figure 8b]), a cluster growth path was identified from Au27 to Au35: from Au27 to Au30 the clusters, which all have a single-atom core, grow by expanding the shell (Au@Aum, m = 26-29); Au33 (Au4@Au29) can be viewed as adding an Au atom to the core of Au32 (Au3@Au29) whereas Au34 (Au4@Au30) can be viewed as adding an Au atom to the shell of Au33 (Au4@Au29). The Au34 structure, featuring a tetrahedral core and a 30-atom shell, is observed to be more round and quite robust, and the Au35 cluster can be viewed as adding an Au atom onto the surface of Au34: [(Au4@Au30) + Au]. The observed core-shell growth path is interesting and may provide a valuable guide to the search for structures of larger gold atomic clusters. It is very excellent agreement with Nan Shao, et al. predictions (28), but their calculation was for the anionic clusters. Nonetheless, there may be some minor discrepancy that may be due to the minimum energy difference between the anionic and neutral clusters (which are more stable).
In Table A, the second column shows that the spectrum ranges vary with respect to the size of the clusters, the shape of the structures, and the arrangement of the atoms (inner core, and the overall outer surface of the edges), as well as the short and the long-range interactions due to the inter-nuclear attraction and the repulsive energies. We have designed a mini formula for the occupancy of the double (D) and the Triple (T) state degeneracy. Interestingly, the double state degeneracy occurred that is influenced by the nearest neighboring atoms, nuclei mass, as well as bond, strength, and their interactions, as well as the zig-zag circumstances of the outermost surface surrounded by them. Surely, we are able to see, the maximum total number of pairs that have occurred on the Au33 cluster among other clusters.
| Table A: The double and the triple state degree of degeneracy of the clusters, Au26-35 at ΔE = 0. | ||||||
| Gold Nanoclusters (AuNCs) |
Point Groups (PG) Symmetry |
Spectral Range (Min - to - Max) ωi [cm-1] |
Double (D) & Triple (T) State Degeneracy [DT]{pairs} |
Total Number of Pairs |
Total Random Number (RN) of Different States of Equal Energy Rn = (D*pairs + T*pairs) |
Predicted Spectral Range Only for D, T- Degeneracies. A: Far Infrared FIR, IR - C 200 - 10 cm-1 B: Mid Infrared MIR, IR - C 3330 - 200 cm-1 X: Lesser than both, A and B |
| Au26 | C1 | 6.58 - 319.61 | D1 T0 | 1 | 2 | A |
| Au27 | C1 | 9.44 - 314.57 | D5 T0 | 5 | 10 | A |
| Au28 | C1 | 3.44 - 347.32 | D5 T0 | 5 | 10 | A |
| Au29 | C1 | 2.34 - 315.87 | D3 T0 | 3 | 6 | A |
| Au30 | C1 | 2.35 - 308.09 | D4 T0 | 4 | 8 | A |
| Au31 | C1 | 8.98 - 322.69 | D6 T0 | 6 | 12 | A |
| Au32 | C1 | 2.43 - 341.62 | D4 T0 | 4 | 8 | A |
| Au33 | D2 | 5.49 - 284.91 | D14 T0 | 14 | 28 | A, B, X |
| Au34 | C1 | 5.06 - 322.42 | D6 T0 | 6 | 12 | A |
| Au35 | C1 | 2.04 - 300.43 | D6 T0 | 6 | 12 | A, X |
General information and its future application of our results
Above all, double-helical gold clusters, researchers can make use of these clusters for the electronic shell-closing ligand-protected gold cluster, because our cluster binds to a central atom to form a coordination complex. Valence states of the triangular and tetrahedral elementary blocks. Both elementary blocks triangular Au3 and tetrahedral Au4 entail only two valence electrons [Au3(2e) and Au4(2e)], thereby both having strong electron shell closures. Wen Wu Xu, et al. clearly shown in their Figures, the two valence electrons were delocalized in the shell-closing elementary blocks [84].
Gold clusters assemble into double-helical super crystals using similar pairing principles to those found between DNA base pairs, scientists have discovered. DNA has previously been used to create helical DNA-nanoparticle hybrid structures, but this was the first time nanoclusters have been known to self-assemble into a double helix. Without help from biological molecules, helices are difficult to build as they require a delicate balance between repulsive and attractive forces - in DNA, these are ionic interactions, and π stacking and hydrogen bonding, respectively [85].
Liganded gold clusters have attracted intensive interest over the past 15 years owing to their broad and practical applications in catalysis [86], electrochemistry [87], quantum electronics [88] and biomedicine [89-92]. A grand challenge to scientists in this field, however, is the precise determination of atomic structures of liganded gold clusters.
Our findings results will definitely help to choose any right suitable candidates (metals or biological molecules) for doping and that will be useful for the future healing of human health diseases and industrial applications.
We are first to present, the vibrational frequencies of medium-sized gold clusters (Au26-35) and the shell-like structure (of course, they are part of the family of so-called full-shell clusters) by using the numerical finite-differentiation method along with the DFTB approach. The DFTB-based calculations work is accomplished to study the gold cluster that is variable with the different sizes. We have observed the vibrational spectrum with excellent accuracy, the starting and the end ranges vary between 2.04 and 347.32 cm−1 at ∆E = 0. Moreover, amazingly the occupancy of the multiple double degeneracies is revealed in all the clusters (refer to Table A). We have compared some of our results, which have an excellent agreement, with the less or availability of the experimental and the theoretical predictions.
In addition to that, we have observed the vibrational properties of the gold clusters in order to explore the stability and the structures. IR spectroscopy is considered the harmonic motion of atoms. Vibrational frequency in the covalent bonding and every covalent bond represents the different specific frequency that vibrates with several modes like scissoring, rocking, and stretching. Above all, we have pinpointed the correct location of the spectrum, through Far Infrared FIR, IR-C 200-10 cm-1, and Mid Infrared MIR, IR-C 3330-200 cm-1. Our prediction will help the researchers to develop a range of potential applications such as catalysis, biomedicine, imaging, optics, and energy conversion. In conclusion, our present calculations of the frequency spectrum are the predictions to be confirmed when the experimental data become available, also, it is expected that this work will be beneficial for the modification of the characteristics of the gold clusters, and further will cause the major development in technological and scientific in the future.
Initially, the main part of this work was strongly supported by the German Research Council (DFG) through project Sp 439/23-1. We gratefully acknowledge their very generous support.
- Yoon B, Häkkinen H, Landman U, Wörz AS, Antonietti JM, Abbet S, Judai K, Heiz U. Charging effects on bonding and catalyzed oxidation of CO on Au8 clusters on MgO. Science. 2005 Jan 21;307(5708):403-7. doi: 10.1126/science.1104168. PMID: 15662008.
- Fielicke A, von Helden G, Meijer G, Pedersen DB, Simard B, Rayner DM. Gold cluster carbonyls: saturated adsorption of CO on gold cluster cations, vibrational spectroscopy, and implications for their structures. J Am Chem Soc. 2005 Jun 15;127(23):8416-23. doi: 10.1021/ja0509230. PMID: 15941275.
- Daniel MC, Astruc D. Gold nanoparticles: assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem Rev. 2004 Jan;104(1):293-346. doi: 10.1021/cr030698+. PMID: 14719978.
- Schwerdtfeger P. Gold goes nano-from small clusters to low-dimensional assemblies. Angew Chem Int Ed Engl. 2003 Apr 29;42(17):1892-5. doi: 10.1002/anie.200201610. PMID: 12730967.
- Chen S, Ingram RS, Hostetler MJ, Pietron JJ, Murray RW, Schaaff TG, Khoury JT, Alvarez MM, Whetten RL. Gold nanoelectrodes of varied size: transition to molecule-like charging. Science. 1998 Jun 26;280(5372):2098-101. doi: 10.1126/science.280.5372.2098. PMID: 9641911.
- Olson RM, Varganov S, Gordon MS, Metiu H, Chretien S, Piecuch P, Kowalski K, Kucharski SA, Musial M. Where does the planar-to-nonplanar turnover occur in small gold clusters? J Am Chem Soc. 2005 Jan 26;127(3):1049-52. doi: 10.1021/ja040197l. PMID: 15656643.
- Häkkinen H, Moseler M, Landman U. Bonding in Cu, Ag, and Au clusters: relativistic effects, trends, and surprises. Phys Rev Lett. 2002 Jul 15;89(3):033401. doi: 10.1103/PhysRevLett.89.033401. Epub 2002 Jun 25. PMID: 12144392.
- Fernández EM, Soler JM, Garzón IL, Balbás LC. Trends in the structure and bonding of noble metal clusters. Phys Rev B. 2004; 70: 165403.
- Gilb S, Jacobsen K, Schooss D, Furche F, Ahlrichs R, Kappes MM. Electronic photodissociation spectroscopy of Aun- . Xe(n=7–11) versus time-dependent density functional theory prediction. J Chem Phys 121, 4619 (2004)
- Furche F, Ahlrichs R, Weis P, Jacob C, Gilb S, Bierweiler T, Kappes MM, The structures of small gold cluster anions as determined by a combination of ion mobility measurements and density functional calculations. Chem J Phys. 2002; 117: 6982.
- Gilb S, Weis P, Furche F, Ahlrichs R, Kappes MM. Structures of small gold cluster cations (Aun+, n<14): Ion mobility measurements versus density functional calculations J Chem Phys. 116, 4094 (2002)
- Häkkinen H, Yoon B, Landman U, Li X, Zhai HJ, Wang LS. On the Electronic and Atomic Structures of Small AuN- (N = 4−14) Clusters: A Photoelectron Spectroscopy and Density-Functional Study. J Phys Chem. 2003; 107: 6168.
- Choi YC, Lee HM, Kim WY, Kwon SK, Nautiyal T, Cheng DY, Vishwanathan K, Kim KS. How can we make stable linear monoatomic chains? Gold-cesium binary subnanowires as an example of a charge-transfer-driven approach to alloying. Phys Rev Lett. 2007 Feb 16;98(7):076101. doi: 10.1103/PhysRevLett.98.076101. Epub 2007 Feb 14. PMID: 17359037.
- Li J, Liu Y, Zhang J, Liang X, Duan H. Density functional theory study of the adsorption of hydrogen atoms on Cu2X (X=3d) clusters. Chem Phys Lett. 2016; 651:137-143.
- Zhang C, Duan H, Lv X, Cao B, Abliz A, Wu Z, Long M. Static and dynamical isomerization of Cu38 cluster. Sci Rep. 2019 May 20;9(1):7564. doi: 10.1038/s41598-019-44055-z. PMID: 31110223; PMCID: PMC6527573.
- Siegel RW. Nanostructured materials-mind over matter. Nanostructured Materials. 1994; 4: 121-138.
- Huang X, Li Z, Yu Z, Deng X, Xin Y. Recent Advances in the Synthesis, Properties, and Biological Applications of Platinum Nanoclusters. Journal of Nanomaterials: 6248725, https://doi.org/10.1155/2019/6248725 2019.
- Allhoff F, Lin P, Moore D. What is nanotechnology and why does it matter?: from science to ethics. Chichester, UK; Malden, MA: Wiley-Blackwell.2010; 293.
- Wang EC, Wang AZ. Nanoparticles and their applications in cell and molecular biology. Integr Biol (Camb). 2014; 6(1): 9-26. doi:10.1039/C3ib40165k
- Hu X, Zhang Y, Ding T, Liu J, Zhao H. Multifunctional Gold Nanoparticles: A Novel Nanomaterial for Various Medical Applications and Biological Activities. Front Bioeng Biotechnol. 2020 Aug 13;8:990. doi: 10.3389/fbioe.2020.00990. PMID: 32903562; PMCID: PMC7438450.
- Kaur N, Aditya RN, Singh A, Kuo TR. Biomedical Applications for Gold Nanoclusters: Recent Developments and Future Perspectives. Nanoscale Res Lett. 2018 Sep 26;13(1):302. doi: 10.1186/s11671-018-2725-9. PMID: 30259230; PMCID: PMC6158143.
- Srinivasa Reddy T, Privér SH, Rao VV, Mirzadeh N, Bhargava SK. Gold(i) and gold(iii) phosphine complexes: synthesis, anticancer activities towards 2D and 3D cancer models, and apoptosis inducing properties. Dalton Trans. 2018 Nov 21;47(43):15312-15323. doi: 10.1039/c8dt01724g. Epub 2018 Sep 6. PMID: 30187047.
- Liu H, Hong G, Luo Z, Chen J, Chang J, Gong M, He H, Yang J, Yuan X, Li L, Mu X, Wang J, Mi W, Luo J, Xie J, Zhang XD. Atomic-Precision Gold Clusters for NIR-II Imaging. Adv Mater. 2019 Nov;31(46):e1901015. doi: 10.1002/adma.201901015. Epub 2019 Oct 1. PMID: 31576632.
- Yue S, Luo M, Liu H, Wei S. Recent Advances of Gold Compounds in Anticancer Immunity. Front Chem. 2020 Jun 30;8:543. doi: 10.3389/fchem.2020.00543. PMID: 32695747; PMCID: PMC7338717.
- Liu Q, Xu C, Wu X, Cheng L. Electronic shells of a tubular Au26 cluster: a cage-cage superatomic molecule based on spherical aromaticity. Nanoscale. 2019 Jul 28;11(28):13227-13232. doi: 10.1039/c9nr02617g. Epub 2019 Jul 9. PMID: 31287479.
- Wang Q, Halet JF, Kahlal S, Muñoz-Castro A, Saillard JY. Electron count and electronic structure of bare icosahedral Au32 and Au33 ionic nanoclusters and ligated derivatives. Stable models with intermediate superatomic shell fillings. Phys Chem Chem Phys. 2020 Sep 23;22(36):20751-20757. doi: 10.1039/d0cp03735d. PMID: 32909020.
- Joshi K, Krishnamurty S. Au26: a case of fluxionality/co-existence. Phys Chem Chem Phys. 2018 Mar 28;20(13):8616-8623. doi: 10.1039/c7cp07997d. PMID: 29479612.
- Shao N, Huang W, Gao Y, Wang LM, Li X, Wang LS, Zeng XC. Probing the structural evolution of medium-sized gold clusters: Aun- (n = 27-35). J Am Chem Soc. 2010 May 12;132(18):6596-605. doi: 10.1021/ja102145g. PMID: 20405837.
- Fa W, Dong J. Possible ground-state structure of Au26: a highly symmetric tubelike cage. J Chem Phys. 2006 Mar 21;124(11):114310. doi: 10.1063/1.2179071. PMID: 16555891.
- Iqbal T, Azam A, Majid A, Zafar M, Shafiq M, Ullah S, Hussien M. A DFT study of electronic, vibrational and optical properties of gold clusters. Optical and Quantum Electronics. 2022; 54:74 https://doi.org/10.1007/s11082-021-03446-1.
- Ji M, Gu X, Li X, Gong X, Li J, Wang LS. Experimental and theoretical investigation of the electronic and geometrical structures of the Au32 cluster. Angew Chem Int Ed Engl. 2005 Nov 4;44(43):7119-23. doi: 10.1002/anie.200502795. PMID: 16217824.
- Jalbout AF, Contreras-Torres FF, Pérez LA, Garzón IL. Low-symmetry structures of Au32Z (Z = +1, 0, -1) clusters. J Phys Chem A. 2008 Jan 24;112(3):353-7. doi: 10.1021/jp074852y. Epub 2008 Jan 1. PMID: 18166025.
- Johansson MP, Vaara J, Sundholm DJ. Exploring the Stability of Golden Fullerenes. Phys Chem C. 2008; 112: 19311.
- Lechtken A, Schooss D, Stairs JR, Blom MN, Furche F, Morgner N, Kostko O, von Issendorff B, Kappes MM. Au34-: a chiral gold cluster? Angew Chem Int Ed Engl. 2007;46(16):2944-8. doi: 10.1002/anie.200604760. PMID: 17348064.
- Doye JPK, Wales DJ. Global minima for transition metal clusters described by Sutton–Chen potentials. New J Chem 1998; 22: 733.
- Gu X, Bulusu S, Li X, Zeng X, Li J. Gong XG, Wang LS. Au34- A Fluxional Core−Shell Cluster. J Phys Chem C. 2007; 111: 8228.
- Santizo IE, Hidalgo F, Perez LA, Noguez C, Garzo´n IL. Intrinsic Chirality in Bare Gold Nanoclusters: The Au34- Case. J Phys Chem C. 2008; 112: 17533.
- Philipp G, Burkhard B, Jonathan T. Lyon, David M. Rayner, and André Fielicke, Far-IR Spectra of Small Neutral Gold Clusters in the Gas Phase. Z Phys Chem. 2014; 228(4-5):337-350.
- Zhou M, Higaki T, Li Y, Zeng C, Li Q, Sfeir MY, Jin R. Three-Stage Evolution from Nonscalable to Scalable Optical Properties of Thiolate-Protected Gold Nanoclusters. J Am Chem Soc. 2019 Dec 18;141(50):19754-19764. doi: 10.1021/jacs.9b09066. Epub 2019 Dec 6. PMID: 31809035.
- Chevrier DM, Chatt A, Zhang P. Properties and applications of protein-stabilized fluorescent gold nanoclusters: short review. J. Nanophoton. 2012;6(1): 064504.
- Mendoza-Huizar LH, Palomar-Pardave M, Robles J. A theoretical quantum study on the distribution of electrophilic and nucleophilic active sites on the Au (100) surface modeled as finite clusters. J. Mol. Struct. (thoechem) 2004;679(3):187-194 .
- Garzón IL, Posada-Amarillas A. Structural and vibrational analysis of amorphous Au55 clusters. Phys Rev B Condens Matter. 1996 Oct 15;54(16):11796-11802. doi: 10.1103/physrevb.54.11796. PMID: 9984971.
- Bravo-Perez G, Garzón IL, Novaro O. Ab initio study of small gold clusters. THEOCHEM. 1999; 493: 225-231.
- Bravo-Perez G, Garzón IL, Novaro O. Non-additive effects in small gold clusters. Chem Phys Lett. 1999; 313: 655-664.
- Sauceda HE, Garzón IL. Structural determination of metal nanoparticles from their vibrational (phonon) density of states. J Phys Chem C. 2015; 119: 10876.
- Sauceda HE, Mongin D, Maioli P, Crut A, Vallee F. Vibrational properties of metal nanoparticles: Atomistic simulation and comparison with time-resolved investigation. J Phys Chem C. 2012; 116: 25147-25156.
- Sauceda HE, Pelayo JJ, Salazar F, Perez LA, Garzón IL. Vibrational spectrum, caloric curve, low-temperature heat capacity, and Debye temperature of sodium clusters: The Na139+case. J Phys Chem C. 2013; 117: 11393-11398.
- Sauceda HE, Salazar F, Perez LA, Garzón IL. Size and shape dependence of the vibrational spectrum and low-temperature specific heat of Au nanoparticles. J Phys Chem C. 2013; 117: 25160-25168.
- Dugan N, Erkoç S. Stability analysis of graphene nanoribbons by molecular dynamics simulations. Phys Stat Sol B. 2008; 245-695.
- Dong Y, Springborg M. Global structure optimization study on Au2-20. Eur Phys J D. 2007; 43: 15-18.
- Warnke I. Heat Capacities of Metal Clusters. Diploma Thesis (Research Assistant and Diploma Research), Saarland University. 2007.
- Dvornikov M. Formulae of numerical differentiation. 2004.
- Seifert G, Schmidt R. Molecular dynamics and trajectory calculations: The application of an LCAO-LDA scheme for simulations of cluster- cluster collisions. New J Chem 1992; 16: 1145.
- Porezag D, Frauenheim T, Köhler T, Seifert G, Kaschner R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys Rev B Condens Matter. 1995 May 15;51(19):12947-12957. doi: 10.1103/physrevb.51.12947. PMID: 9978089.
- Seifert G, Porezag D, Frauenheim TH. Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme. Int J Quantum Chem 1996; 58: 185-189.
- Seifert G. Tight-binding density functional theory: an approximate Kohn-Sham DFT scheme. J Phys Chem A. 2007 Jul 5;111(26):5609-13. doi: 10.1021/jp069056r. Epub 2007 Apr 18. PMID: 17439198.
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran. Cambridge University Press. 2007.
- Theoretical Studies of Properties of Low-Dimensional Systems: Clusters and Conjugated Polymers, PhD thesis, Yi Dong, Saarland University, Germany. 2006.
- Dong Y, Springborg M, Unbiased Determination of Structural and Electronic Properties of Gold Clusters with up to 58 Atoms, The Journal of Physical Chemistry C. 2007; 111;(34): 12528-12535, DOI: 10.1021/jp071120x
- Vishwanathan K. Effect of Size, Temperature, and Structure on the Vibrational Heat Capacity of Small Neutral Gold Clusters. J Material Sci Eng. 2017; 6: 325. doi: 10.4172/2169-0022.1000325.
- Vishwanathan K. Bonding Forces and Energies on the Potential Energy Surface (PES) of the Optimized Gold Atomic Clusters by a Differentiation Step-Size (ds = ± 0.01 a.u.)via DFTB Method. Nanosci Technol. 2018; 5:1-4.
- Ijaz M, Aftab M, Afsheen S, Iqbal T. Novel Au nano-grating for detection of water in various electrolytes. Appl Nanosci. 2020; 10(11): 4029-4036.
- Ijaz M, Zafar M, Afsheen S, Iqbal T. A review on Ag-nanostructures for enhancement in shelf time of fruits. J Inorg Organomet. Polym Mater. 2020;30(5):1475-1482.
- Fielicke A, Kirilyuk A, Ratsch C, Behler J, Scheffler M, von Helden G, Meijer G. Structure determination of isolated metal clusters via far-infrared spectroscopy. Phys Rev Lett. 2004 Jul 9;93(2):023401. doi: 10.1103/PhysRevLett.93.023401. Epub 2004 Jul 7. PMID: 15323913.
- Ratsch C, Fielicke A, Kirilyuk A, Behler J, von Helden G, Meijer G, Scheffler M. Structure determination of small vanadium clusters by density-functional theory in comparison with experimental far-infrared spectra. J Chem Phys. 2005 Mar 22;122(12):124302. doi: 10.1063/1.1862621. PMID: 15836373.
- Fielicke A, Ratsch C, von Helden G, Meijer G. Isomer selective infrared spectroscopy of neutral metal clusters. J Chem Phys. 2005 Mar 1;122(9):091105. doi: 10.1063/1.1872834. PMID: 15836105.
- Nhat PV, Si NT, Nguyen MT. Structural Evolution and Stability Trend of Small-Sized Gold Clusters Aun (n = 20-30). J Phys Chem A. 2020 Feb 20;124(7):1289-1299. doi: 10.1021/acs.jpca.9b09287. Epub 2020 Feb 7. PMID: 31990548.
- Nhat PV, Si NT, Kiselev VG, Nguyen MT. Another look at energetically quasi-degenerate structures of the gold cluster Au27q with q = 1, 0, -1. J Comput Chem. 2021 Nov 15;42(30):2145-2153. doi: 10.1002/jcc.26744. Epub 2021 Aug 26. PMID: 34435682.
- Knoppe S, Malola S, Lehtovaara L, Bürgi T, Häkkinen H. Electronic structure and optical properties of the thiolate-protected Au28(SMe)20 cluster. J Phys Chem A. 2013 Oct 10;117(40):10526-33. doi: 10.1021/jp407494v. Epub 2013 Sep 30. PMID: 24032562.
- Wang S, Xiong L, Sun G, Tang L, Zhang J, Pei Y, Zhu M. The mechanism of metal exchange in non-metallic nanoclusters. Nanoscale Adv. 2020 Jan 14;2(2):664-668. doi: 10.1039/c9na00746f. PMID: 36133226; PMCID: PMC9419833.
- Xiong L, Peng B, Ma Z, Wang P, Pei Y. A ten-electron (10e) thiolate-protected Au29(SR)19 cluster: structure prediction and a 'gold-atom insertion, thiolate-group elimination' mechanism. Nanoscale. 2017 Feb 23;9(8):2895-2902. doi: 10.1039/c6nr09612c. PMID: 28177034.
- Johansson MP, Sundholm D, Vaara J. Au32: a 24-carat golden fullerene. Angew Chem Int Ed Engl. 2004 May 10;43(20):2678-81. doi: 10.1002/anie.200453986. PMID: 18629988.
- Gu X, Ji M, Wei HS, Gong XG. AuN clusters (N = 32, 33, 34, 35): Cagelike structures of pure metal atoms. Phys Rev. B 70. 205401. 2004.
- Hirsch A, Chen Z, Jiao H. Spherical Aromaticity in Ih Symmetrical Fullerenes: The 2(N+1)2 Rule. Angew Chem Int Ed Engl. 2000 Nov 3;39(21):3915-3917. doi: 10.1002/1521-3773(20001103)39:21<3915::AID-ANIE3915>3.0.CO;2-O. PMID: 29711706.
- Gao Y, Bulusu S, Zeng XC. Gold-caged metal clusters with large HOMO-LUMO gap and high electron affinity. J Am Chem Soc. 2005 Nov 16;127(45):15680-1. doi: 10.1021/ja055407o. PMID: 16277491.
- Fa W, Zhou J, Luo C, Dong J, Cage-like Au32 detected by calculated optical spectroscopy. arXiv preprint cond-mat/0507570.2005.
- Johansson MP, Sundholm D, Vaara J. Au32: a 24-carat golden fullerene. Angew Chem Int Ed Engl. 2004 May 10;43(20):2678-81. doi: 10.1002/anie.200453986. PMID: 18629988.
- Majid A, Fatima S, Dar A. A density functional theory study of electronic properties of Ce: GaN. Comput. Mater. Sci. 2013;79: 929-932.
- Majid A, Batool A, Khan SUD, Haider S. First-principles study of vibrational properties of TiSiO4 clusters. Int J Quant. Chem. 2019; 119 :(14). e25924 .
- Majid A, Jabeen A, Khan SUD, Haider S. First principles investigations of vibrational properties of titania and zirconia clusters. J Nanopart Res. 2019; 21(1): 20.
- Gu X, Bulusu S, Li X, Zeng XC, Li J, Gong XG, Wang LS. Au34-: A Fluxional Core-Shell Cluster, The Journal of Physical Chemistry C. 2007; 111;(23): 8228-8232. DOI: 10.1021/jp071960b
- Santizo IE, Hidalgo F, Pérez LA, Noguez C, Garzón IL. Intrinsic Chirality in Bare Gold Nanoclusters: The Au34− Case. The Journal of Physical Chemistry C. 2008; 112;(45): 17533-17539. DOI: 10.1021/jp806080b
- Vargas A, Santarossa G, Inannuzzi M, Baiker A. Fluxionality of gold nanoparticles investigated by Born-Oppenheimer molecular dynamics. Phys Rev B. 2009; 80: 195421.
- Xu WW, Zhu B, Zeng XC, Gao Y. A grand unified model for liganded gold clusters. Nat Commun. 2016 Dec 2;7:13574. doi: 10.1038/ncomms13574. PMID: 27910848; PMCID: PMC5146290.
- Li Y. Gold double helix assembles with DNA-like precision. Nature. 2021; 594-380 (DOI: 10.1038/s41586-021-03564-6)
- Turner M, Golovko VB, Vaughan OP, Abdulkin P, Berenguer-Murcia A, Tikhov MS, Johnson BF, Lambert RM. Selective oxidation with dioxygen by gold nanoparticle catalysts derived from 55-atom clusters. Nature. 2008 Aug 21;454(7207):981-3. doi: 10.1038/nature07194. PMID: 18719586.
- Chen S, Ingram RS, Hostetler MJ, Pietron JJ, Murray RW, Schaaff TG, Khoury JT, Alvarez MM, Whetten RL. Gold nanoelectrodes of varied size: transition to molecule-like charging. Science. 1998 Jun 26;280(5372):2098-101. doi: 10.1126/science.280.5372.2098. PMID: 9641911.
- Daniel MC, Astruc D. Gold nanoparticles: assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem Rev. 2004 Jan;104(1):293-346. doi: 10.1021/cr030698+. PMID: 14719978.
- Rosi NL, Giljohann DA, Thaxton CS, Lytton-Jean AK, Han MS, Mirkin CA. Oligonucleotide-modified gold nanoparticles for intracellular gene regulation. Science. 2006 May 19;312(5776):1027-30. doi: 10.1126/science.1125559. PMID: 16709779.
- Vishwanathan K. A Medium-Sized Nanoclusters Au38 (C1): A Numerical Finite-Difference Method with DFTB Approach. Journal of Modern Technology and Engineering. 2021; 89-103.
- Vishwanathan K. Au25: A Tip-enhanced, Spinning Top - Core-Shell? The Brightest Molecular Super Star among the Nanoclusters, Au21-25. Advanced Physical Research, 2021;19-34.doi:10.21203/rs.3.rs-77919/v1
- Vishwanathan K. DFTB Calculations of a shapeless Au55 (C1) nanoclusters, New Materials, Compounds and Applications. 2019; 53-76.