More Information
Submitted: August 08, 2023 | Approved: August 28, 2023 | Published: August 29, 2023
How to cite this article: Abrukov VS, Konnova KA, Egorov EN, Anufrieva DA, Koltsov NI. Neural Network Calculator of Rubber Characteristics with Improved Properties. Ann Adv Chem. 2023; 7: 064-067.
DOI: 10.29328/journal.aac.1001045
Copyright License: © 2023 Abrukov VS, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Artificial neural networks; Rubber compound; Vulcanizates; Basalt fiber; Physical and mechanical properties
Neural Network Calculator of Rubber Characteristics with Improved Properties
VS Abrukov*, KA Konnova, EN Egorov, DA Anufrieva and NI Koltsov
Chuvash State University I.N. Ulyanova, Cheboksary, Russia
*Address for Correspondence: VS Abrukov, Chuvash State University I.N. Ulyanova, Cheboksary, Russia, Email: [email protected]
A new technique for the use of Artificial Neural Networks (ANN) for the generalization and visual presentation of the results of experimental studies is proposed. The possibility of using ANN for cases for which their use was previously considered impossible is shown. ANN calculators have been created that summarize the results of experimental studies on the effect of trans-polynorbornene and basalt fiber on the characteristics of a rubber compound based on general-purpose rubbers (isoprene SKI-3, butadiene-methylstyrene SKMS-30ARK and butadiene SKD), which also contained vulcanizing agents (N, N′-dithiodimorpholine, thiuram D), vulcanization accelerators (sulfenamide C, 2-mercapto-benzothiazole), vulcanization activators (zinc white, stearic acid), emollients (industrial oil I-12A, rosin) and antioxidants (acetonanil H, diaphene FP). The rubber mixture was prepared on laboratory rollers LB 320 160/160. Subsequently, the rubber mixture was vulcanized in a P-V-100-3RT-2-PCD press. For the resulting vulcanizates, the physical and mechanical properties and their changes were determined after daily exposure to air and in a standard SZhR-1 hydrocarbon liquid at a temperature of 100 °C. We also studied the change in the mass of vulcanizates after exposure to industrial oil I-20A and water. The dynamic parameters (modulus of elasticity and mechanical loss tangent) of vulcanizates, which characterize their noise and vibration-absorbing properties, were studied on a Metravib VHF 104 dynamic mechanical analyzer. The created ANN calculators allow solving a direct problem - interpolating the dependences of all rubber characteristics on the content of basalt fiber, as well as solving inverse problems - to determine the required content of basalt fiber to create rubber with the required performance properties. The autonomous executable modules of the calculators developed by ANN were made and can be passed to everyone.
It is known that the movement of railway transport creates noise and vibration that has a negative impact on the environment and people. To reduce them, highly elastic rubber pads of rail fasteners are used, which are shock absorbers that reduce resonant vibrations of railway tracks during train movement [1]. To improve the performance properties of rail pads, it is necessary to develop rubber compound formulations through the use of special additives. These include trans-polynorbornene (trans-polybicyclo [2,2,1] hept-2-ene) [2,3], the possibility of using which for rail fasteners was studied in [4,5] to improve sound and vibration absorption. rubber properties. Vibration-absorbing materials also include polymer compositions containing fibrous fillers. One of these fillers is basalt fiber [6]. It is of interest to investigate the combined effect of Trans-Polynorbornene (TPNB) and basalt fiber on the properties of rubber gaskets. The purpose of this work was an experimental study of the effect of TPNB and basalt fiber on the properties of rubber and the creation of a neural network calculator that allows interpolating the experimental results and determining the formulation of a rubber mixture with specified performance properties.
The studied rubber mixture contained general-purpose rubbers (isoprene SKI-3, butadiene-methylstyrene SKMS-30ARK and butadiene SKD), vulcanizing agents (N, N′-dithiodimorpholine, thiuram D), vulcanization accelerators (sulfenamide C, 2-mercaptobenzothiazole), vulcanization activators (zinc white, stearic acid), softeners (industrial oil I-12A, rosin), antioxidants (acetonanil N, diaphen FP) and others). The rubber mixture was prepared on laboratory rolls LB 320 160/160 at a temperature of the rolls of the rolls of 60 °C - 70 °C for 15 min. Subsequently, the rubber mixture was vulcanized in a P-V-100-3RT-2-PCD vulcanizing press at a temperature of 143 °C for 25 min. For the resulting vulcanizates, the physical and mechanical properties and their changes after daily exposure to air and in the standard hydrocarbon liquid SZHR-1 at a temperature of 100 °C were determined, and the change in the mass of vulcanizates after exposure to industrial oil I-20A and water at a temperature of 23 °C with within 24 hours was studied. The dynamic parameters (modulus of elasticity and mechanical loss tangent) of vulcanizates, which characterize the noise and vibration-absorbing properties of vulcanizates, were studied on a Metravib VHF 104 dynamic mechanical analyzer at a degree of deformation of 0.01%, a temperature of 30 °C, and a frequency of 1000 Hz. The basalt fiber was a staple with a cutting length of 10 mm - 12 mm and an elementary fiber diameter of 9 - 13 μm. Norsorex APX TPNB was a fine-grained white powder with a particle size of 300 - 400 µm and a bulk density of 0.35 - 0.40 g/cm3. To improve the compatibility of TPNB with the rubber matrix, a rubber-like composition of TPNB was developed with a technological additive - industrial oil I-12A at a mass ratio of 1:1. Subsequently, the resulting TPNB composition was introduced into the rubber mixture, the content of which in all the studied variants was 50.0 wt. h. per 100.0 wt. h. rubbers. At the same time, the first (basic) version of the rubber mixture did not contain basalt fiber, and the second - fifth versions of the mixture were prepared using basalt fiber in an amount from 2.0 to 10.0 wt. h. 100.0 wt. h. rubbers. The results of the options and properties of the studied rubber mixture are presented in the Table 1.
| Table 1: Variants and properties of the studied rubber compound. | ||||||
| Ingredients, indicators | Rubber compound options | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Composition of TPNB with industrial oil I-12A, wt. h. | 50.0 | 50.0 | 50.0 | 50.0 | 50.0 | 50.0 |
| Basalt fiber, wt. h. | - | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 |
| Physical and mechanical properties of vulcanizates | ||||||
| f100, MPa | 5.3 | 5.3 | 5.5 | 5.8 | 6.0 | 6.3 |
| fp, MPa | 15.2 | 15.5 | 15.7 | 15.8 | 16.1 | 16.3 |
| εp, % | 470 | 460 | 460 | 450 | 440 | 420 |
| H, unit Shore A | 72 | 74 | 76 | 78 | 79 | 81 |
| В, кН/м | 38 | 41 | 44 | 45 | 47 | 49 |
| ODS at 30% compression (100 °С × 24 ч), % |
43.8 | 42.6 | 41.9 | 41.1 | 41.4 | 39.7 |
| α, m3/TJ | 58.3 | 57.1 | 55.7 | 53.4 | 51.6 | 50.2 |
| Changes in the physical and mechanical properties of vulcanizates after air aging |
||||||
| ∆fp, % | -7.9 | -7.1 | -6.7 | -6.8 | -6.3 | -5.9 |
| ∆eр, % | -33.4 | -35.5 | -32.4 | -31.1 | -30.3 | -30.4 |
| ΔH, units Shore A | +2 | +1 | +2 | +2 | +1 | +1 |
| Changes in the physical and mechanical properties of vulcanizates after exposure to SZHR-1 (100 °C × 24 hours) |
||||||
| Δfp, % | -24,8 | -23,5 | -21,8 | -22,7 | -20,9 | -19,6 |
| Δεp, % | -27,7 | -26,2 | -24,8 | -23,6 | -22,3 | -21,5 |
| ΔH, units Shore A | -8 | -8 | -7 | -5 | -4 | -4 |
| Dynamic properties of vulcanizates | ||||||
| E′·10-7, Па | 4.51 | 5.02 | 5.12 | 5.31 | 5.86 | 6.64 |
| tgδ | 0.214 | 0.225 | 0.226 | 0.228 | 0.230 | 0.232 |
| Note: f100 - Conditional stress at 100% tension; fp - Conditional tensile strength; eр - Relative elongation at break; H - hardness; B - Tear resistance; RDS - Relative residual static compression strain; α - Abrasion; ∆fp, ∆eр - Relative change in conditional tensile strength and relative elongation at break; ∆H is the difference in rubber hardness after and before exposure to an aggressive environment; E' is the modulus of elasticity; tgδ is the tangent of the mechanical loss angle. | ||||||
To summarize all the dependencies contained in the table, Artificial Neural Networks (ANN) were used, the rules and examples of their application are given in [7] and with various figures and graphs in [8-12]. One of the main rules of using ANN is that in order to generalize the patterns of an experiment with a large number of variables, a very large number of examples with different data sets is required. Violation of this rule leads to the so-called retraining of the ANN. It is believed that this makes it impossible to use the ANN when summarizing the results of experimental studies.
In this article, the number of examples - sets of variable values is small, only 6 (six values of the content of basalt fiber in the mixture and, accordingly, 6 values of the characteristics of various physical, mechanical, and other properties of the rubber mixture). However, we used ANN to generalize the results of these experiments and created an ANN calculator, the results of which are given below, which showed the possibility of using ANN to interpolate experimental results in the case of a small number of examples.
To create an ANN calculator, the domestic analytical platform Deductor (www.basegroup.ru) was used, the results of which are given in [9-13].
The structure of the ANN calculator for solving the direct problem, corresponding to the experimental data given in the table, was as follows. One neuron in the input layer of the ANN (the only input variable was the content of basalt fiber - BF), 12 neurons in the output layer (12 main characteristics of physical-mechanical and dynamic properties are given in the Table), one inner (hidden) layer - 6 neurons.
This structure, as well as others, can be seen in the autonomous executable modules of the calculators developed by ANN located at [7]. This module comes with instructions for use. A summary of ANN theory and other various ANN structures is given in [13].
The assessment of the accuracy of the obtained ANN calculator showed that the root-mean-square error of calculations is in the range of 7.1 10-5 ... 3.7 10-3 depending on the calculated characteristic (in units of a specific characteristic). The relative interpolation error, depending on the calculated characteristic, ranges from 0 (up to the 4th digit) to 1%.
Figure 1 shows a screenshot of the screen of a neural net-work calculator, which shows the values of the characteristics of the physical-mechanical and dynamic properties of vulcanizates with a content of basalt fiber in the amount of 6 wt. h.
Figure 1: Screenshot of the neural network calculator when solving a direct problem.
Comparing these values with the values given in the table, one can estimate the absolute and relative error in the calculation of each specific characteristic. These estimates show that the ANN calculator accurately calculates the characteristics of the physical-mechanical and dynamic properties of vulcanizates.
At the same time, following [8], it cannot be argued that real experimental data can be considered as reference, that is, more accurate. The high “smoothing” abilities of the ANN when approximating experimental data burdened with measurement errors and revealing hidden dependencies in the data in some cases allow us to state that the ANN calculations better reflect the real dependences of the experiment, in our case, the real dependences of the characteristics of physical, mechanical and dynamic properties of vulcanizates on the content of basalt fiber. This issue requires further research.
The work of the ANN calculator in solving the direct problem from the point of view of interpolation of experimental results is illustrated in Figure 2, which presents the results of calculating the characteristics of the physical-mechanical and dynamic properties of vulcanizates with the content of basalt fiber equal to 7 wt. h. Real measurements of such a content of basalt fiber were not carried out.
Figure 2: Screenshot of the neural network calculator when solving a direct problem in terms of interpolation.
We also created ANN calculators for solving inverse problems, which are formulated as follows: What should be the content of basalt fiber in order to obtain the specified values of the characteristics of the physical and mechanical properties of vulcanizates? The structure of one of the ANN calculators was as follows: three neurons in the input layer of the ANN (given values of three characteristics of the physical and mechanical properties of vulcanizates, 1 neuron in the output layer (amount of basalt fiber), and one inner (hidden) layer - 6 neurons.
This structure, as well as others, can be seen in the autonomous executable modules of the calculators developed by ANN located at [11].
Figure 3 presents the result of solving the inverse problem in the form of a screenshot of the ANN calculator screen, which shows that the specified values of the characteristics of the physical and mechanical properties of vulcanizates (“input values”) provide the content of basalt fiber (“output values”), equal to approximately 6.06 mass. h. The results of assessing the accuracy of the ANN calculator showed that it has a high accuracy, the root-mean-square error of calculating the BV is in the range of 8.1 10-4 ... 2.4 10-3 wt. h.
Figure 3: Screenshot of the ANN calculator for solving the inverse problem.
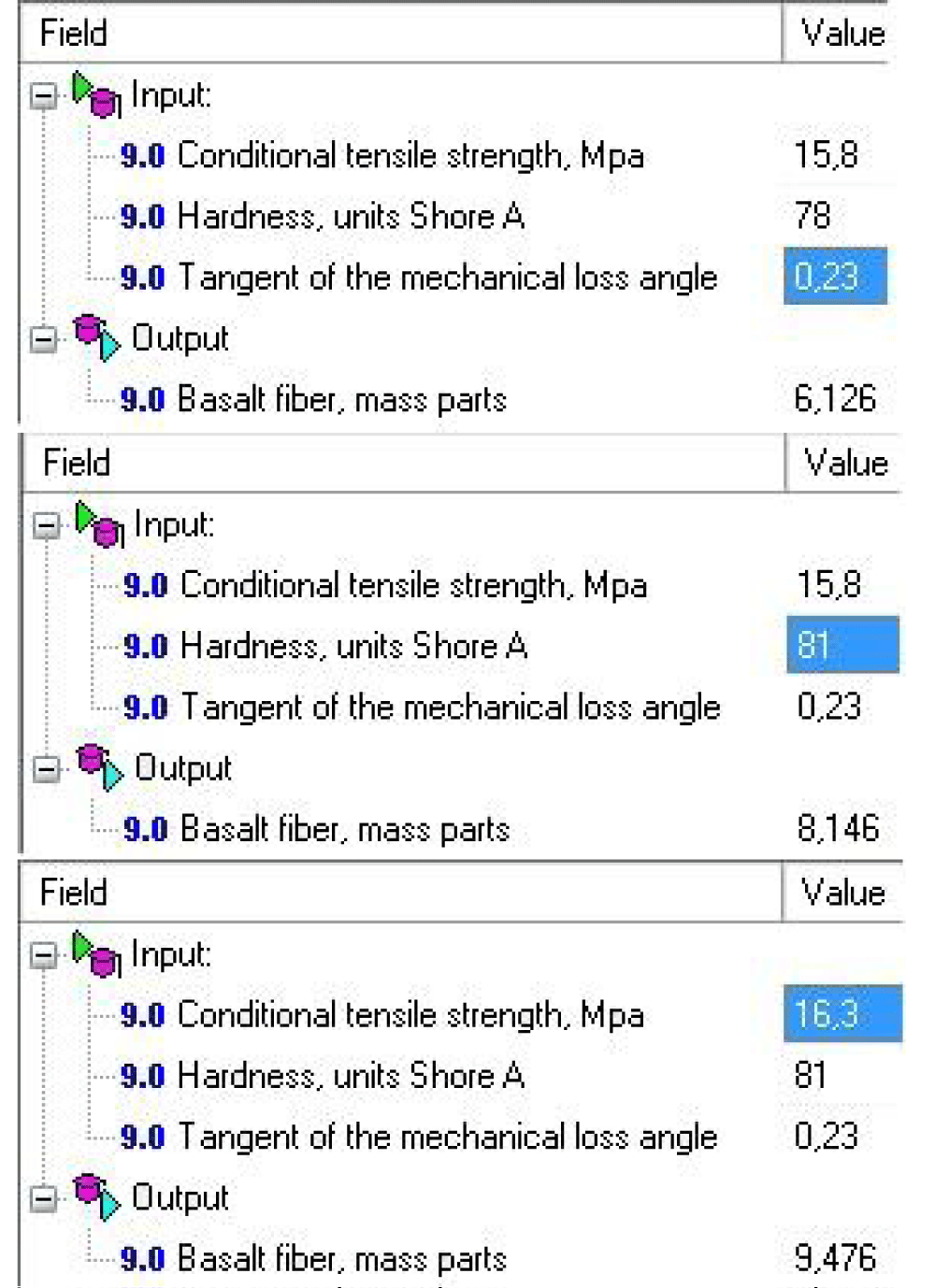
The operation of this ANN calculator is illustrated in Figure 4. The screenshots below show the results of calculating the amount of basalt fiber, which provides three different sets of values for the characteristics of the physical and mechanical properties of vulcanizates.
Figure 4: Screenshots of the ANN calculator screens for solving the inverse problem of calculating the amount of basalt fiber, which provides different sets of values for the characteristics of the physical and mechanical properties of vulcanizates.
A new technique for the use of Artificial Neural Networks (ANN) for a generalized and visual representation of the results of experimental studies is proposed. ANN calculators have been created that summarize with sufficiently high accuracy the results of experimental studies on the effect of trans-polynorbornene and basalt fiber on the characteristics of a rubber compound based on general-purpose rubbers. The ANN calculator allows solving the direct problem - to interpolate the dependences of all rubber characteristics on the content of basalt fiber, as well as the inverse problem - to determine the required content of basalt fiber to create rubber with the required performance properties. The autonomous executable modules of the calculators developed by ANN were made and can be passed to everyone.
- Butorina MV, Ivanov PV, Petryaev AV. Reducing the vibroacoustic impact of high-speed trains. 2018; 7:15-19.
- Çakmak UD, Hiptmair F, Major Z. Applicability of elastomer time-dependent behavior in dynamic mechanical damping systems // Mechanics of Time-Depend Materials. 2014; 18:1; 139-151.
- Xu J, Li A, Wang H, Shen Y. Dynamic mechanical analysis of Norsorex/acrylonitrile butadiene rubber blends and their application in vibration control of steel frames // Advances in Mechanical Eng. 2016; 8:8; 1-16.
- Pat. RU 2739188. 2020.
- Egorov EN, Ushmarin NF, Sandalov SI, Koltsov NI. Development, and study of a rubber compound for rail fasteners, Ross. chem. magazine (Journal Ross. Chemical Society named after D.I. Mendeleev). 2021; 65:1; 56-61.
- Litus AA, Sinitsyna IN, Artemenko SE, Zemlyansky AA. Noise-absorbing and sound-proof materials based on basalt fibers // Plastic masses. 2008; 1:25-27.
- Abrukov V, Anufrieva D, Koltsov N. Neural network calculator of rubber characteristics with improved properties. https://www.researchgate.net/publication/359716811_Neural_network_calculator_of_rubber_characteristics_with_improved_properties (accessed 03/20/2022).
- Abrukov V, Kiselev M, Gulseren O, Anufrieva D. Artificial Neural Networks is Methodological Basis of a Nano Materials Genome. https://www.researchgate.net/publication/351461911_Artificial_Neural_Networks_is_Methodological_Basis_of_a_Nano_Materials_Genome (accessed 03/20/2022).
- Mariappan A, Choi H, Abrukov V, Lukin A, Sankar V, Sanal Kumar VR. The application of energetic materials genome approach for the development of the solid propellants through the space debris recycling at the space platform // AIAA Propulsion and Energy 2020 Forum: Conference Proceeding, Virtual, Online: American Institute of Aeronautics and Astronautics Inc, AIAA, 24- 28 August 2020. AIAA 2020-3898.
- Abrukov V, Lukin A, Oommen C, Sanal Kumar VR, Chandrasekaran N, Sankar V, Kiselev M, Anufrieva D. Development of the Multifactorial Computational Models of the Solid Propellants Combustion by Means of Data Science Methods - Phase III. // Technology and Investment, 2019, Proceedings of the 55th AIAA/SAE/ASEE Joint Propulsion Conference 2019, AIAA Propulsion and Energy Forum, Indianapolis, Indiana. 19-22 August 2019; AIAA 2019-3957.
- Abrukov V, Lukin A, Oommen C, Chandrasekaran N, Bharath R, Sanal Kumar VR, Kiselev V, Anufrieva D. Development of the Multifactorial Computational Models of the Solid Propellants Combustion by Means of Data Science Methods – Phase II. Technology and Investment, 2018, Proceedings of a meeting held 9-11 July 2018; Cincinnati, Ohio, USA. Held at the AIAA Propulsion and Energy Forum 2018 - AIAA 2018-4961.
- Abrukov V, Kochakov V, Smirnov A, Abrukov S, Anufrieva D. Knowledge-based system is a goal and a tool for basic and applied research. // 9th International Conference on Application of Information and Communication Technologies, AICT 2015 - Proceedings: 9, Rostov-on-Don, 14–16 October 2015; 60-63.
- Pang W, Abrukov V, Anufrieva D, Chen D. Burning Rate Prediction of Solid Rocket Propellant (SRP) with High-Energy Materials Genome (HEMG). Crystals 2023; 13:237. https://doi.org/10.3390/cryst13020237