Techno-econophysics’ Fractal Involving of Exergy Remarks

Inclusively new to econophysics studies, herewith proposed technoeconophysics as part of techno-economy, econophysics & sociophysics to interpret the description between probability and hypothesis found between fractal realms and econophysics of markets, physics markets, or stock markets any chaotic evidence [exergy destructive] could present if effective & efficient criterion doesn’t comply. A more precise iterative study ought to be held to configure how fractal dimension is involved in the techno-econophysics study of the Helium Nat Gas Project which is not integer, but also proofed numerically & analytically.

Econophysics, which emerged over a decade ago, applies various models and concepts associated with statistical physics to economic (and financial) phenomena. Econophysics can reduce some of the uncertainty that is ignored in economics. In this perspective, econophysics is considered a Knightian method of reducing uncertainty. This method will also be presented as a complementary approach to the Hayekian framework [1,2]. Some physicists claim their modeling & data analysis can change the way we view stock markets but mainstream economists have yet to be convinced [3].

Ever concluded this week’s lottery numbers can be predicted by identifying hidden patterns of previous draws, standard economic theory similarly pours cold water on the idea that the behavior of stock markets affected by past market movements. The future behavior of a market depends only on events in the real world, such as profits & losses made by individual companies. Further, some economists argued that past trading does seem to have subtle effects on future fluctuations. Others in the new field of ‘behavioral economics’ suggest that the irrational psychology of investors lies behind these trends followed by some surprising allies: physicists intent on revealing hidden patterns in market behavior in the field known as econophysics.

For much of the 20^th century, economists believed that the probability of a given change in the value of most markets – such as stock or foreign-currency exchange – followed a pattern known as a bell curve. This curve has two important properties: averaged over time, the most likely change is zero, and, because the curve tails off rapidly in extreme values, the probability of large fluctuations occurring is very low. Average stock prices may increase or decrease over the long term, but day-to-day fluctuations seem to follow the bell curve.

Analysis of the data, however, shows that market behavior is subtly different. In the 1960s, Mandelbrot & Fama showed that markets are better described by power-law distributions (Mandelbrot, 1963 & Fama, 1965).

On behalf of “Helium Nat Gas Project” beheld as Astranomics [completes carbon-based economy, hydrogen economy, thermoeconomics, etc.] affiliated with helium, propylene extraction & processing from natural gas accompanying KG-Media as Associate-Company, we also quote Kuznetsov & Mandel (2005) of Metaphysics: “part of sociophysics, studying processes of mass communications in social & sociobiological systems”, in terms of econophysics of the project.

Fractal involving econophysics of markets

One of the great innovations in finance coming from econophysics is the fractal market hypothesis, which contradicts the traditional efficient market hypothesis [4]. It is commonly accepted that the second law of thermodynamics states that all systems left to the natural conditions in the universe will evolve toward entropy, disorganization, and disruption over time [5]. The transition from a regular, organized, and planned structure of a social system to an irregular, disorganized, and unplanned state will increase its entropy, and the increase in the irregularity of a system will lead to the increase in the entropy of that system at the same rate.

In macro-sociophysics, communities in society were considered as elements. Later, in the micro-sociophysics dimensions, the association of individuals in the relevant communities and then the behavior of the laws of physics began to emerge.

Here described a mathematic (or statistical physics) technique to analyze population distribution between two or many alternatives [6]. In Blenkinsop (2004) the number of squares N(r) of side r necessary to cover all the deposits (alternatively the number of squares containing one or more deposits) is measured as a function of r. In fractal geometry

N(r) ~ r – Db (1)

Where Db is the box-counting fractal dimensions [7]. To correlate it to expression in Green function [in Metaphysics/sociophysics description], we introduce

N(r) ~ 1/r^Db especially if Db = 1, N(r) ~ 1/r. (2)

Taking into account r as a single variable, its differentiation concerning r, dN(r)/dr can be seen as multiplication with [1/r]

So ∇_r = 1/ r.

Further, in the relationship between Feigenbaum’s constant a & power spectra [8], the normalized variance [1/a²ⁿ] represents the statistical probability density of the n^th step growth whereas

[Prob]_n = [1/a²ⁿ] = τ ^-4n or [Prob]_n = τ^-4t (3)

Where t is the normalized standard deviation and

τ² = a = 2.62 whereas τ = √2.62 = 1.61864140562

Now in the application of fractals in Metaphysics, we compare to the transfer operator [Kuznetsov & Mandel]:

Q = exp [-W_t+1 (q)]. G

Where we know: d/dx [e^x] = e^x and further ∇_x [e^x] = e^x

Enhancement of helium Nat gas project

Ever concluded whereas helium recovery & extraction at least fulfill cost-effective calculations, prices of sales gas and helium can be cumulated/summed up without depreciating the energy content of natural gas.

Further, the economic threshold of 0.05% helium contained in nat gas can benefit a four times adding factor through 0.05% - 0.2% to 80 times through 0.05 - 4.0 cost enhancement, which is then analyzed by discrete Gaussian kernel curve.

The cost-effective reasons ought to be followed by a cost-efficient analysis that firstly takes into account through a techno-economic analysis where equipment cost estimation is calculated by historical cost method or using pieces of information from previous projects with similar specifications, which after listing each equipment cost, Guthrie method is used to calculate the total cost for an installation [9].

In general, we can adopt the Gauge Theory of Arbitrage [10] in which the consideration maps the capital market into QED [Quantum Electro Dynamics] i.e. a quantum system of particles with positive (securities) and negative (“debts”) charges which interact with each other through the electromagnetic field (gauge field of the arbitrage).

Toward the techno-econophysics study, herewith adopted the exergy of available energy concept description in the optimization study of LNG boil-off gas [11] to follow the exergy analysis developed by Kamran Taheri [2014].

The economic process from cost-effective & cost-efficient criteria discussed here a little [exergy is a concept of energy efficiency optimized processes ]whereas to that process it could be any fractal involved in techno-econophysics study as compared by Guang Liu [12].

According to the theory of Mandelbrot (1970, 1971), for any fractal Brownian motion B_H (t), the correlation CN between the yields of securities can be expressed by

CN = 2^2H-1 -1 (4)

Where H denotes the Hurst exponent.

If H =1/2, then CN = 0, and B_H (t) is equal to the standard Brownian motion which indicates that the yields of securities are random & unrelated.

If ½ < H < 1 and 0< H < ½ then CN > 0 & CN < 0 and B_H (t) is equal to fractal Brownian motion.

Comparing equations 3 & 4 of course correlation coefficients are not the same as probability. R-squared measures the amount of variation in one variable that can be expressed by another variable whereas probability is a measure of the likelihood of an event occurring.

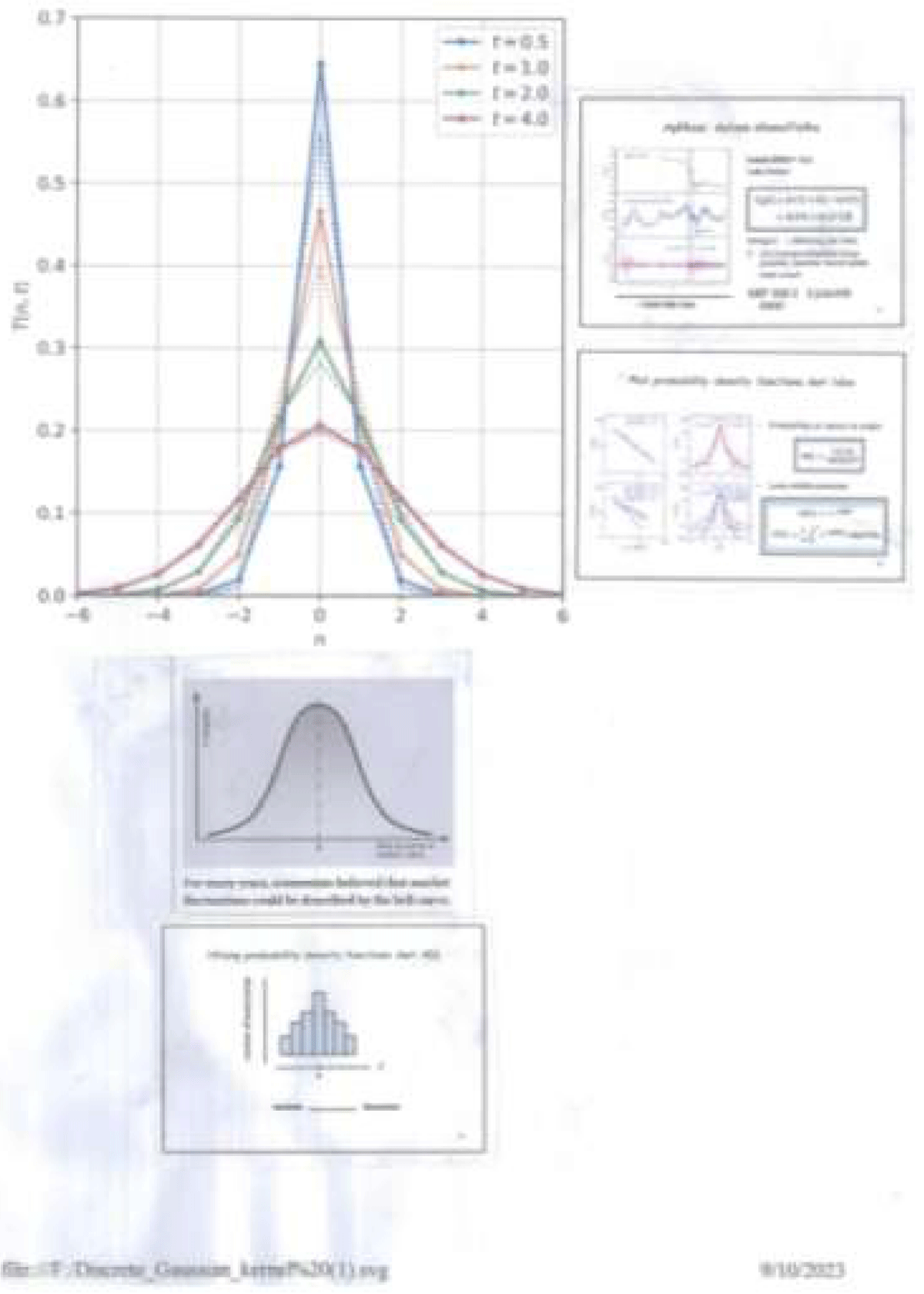
Configuratively compared to the description from the histogram to the application of econophysics in Figure 1, the study of the Efficient Market Hypothesis & Fractal Market Hypothesis for example followed by its relation to two power-laws [13] a continuation of the study of fractals & scaling in finance [14] further predicted any chaotic evidence (exergy destructive) would occur if cost-effective & cost-efficient criterion doesn’t comply.

The cost-efficient criteria above are considered in exergy analysis as a developed concept of energy efficiency optimized processes [15] which optimization measures such as making efficient use of energy or something. Given the global economic growth and rapid manufacturing development, energy and resource efficiency will become an increasingly competitive factor and scope for companies on the road to sustainability. Among energy efficiency optimization approaches, thermodynamic methodologies contribute toward the improvement of energy efficiency in manufacturing processes. Besides energy balance, exergy has been recently considered as a practical thermodynamic method for a system’s energy evaluation and used to manage hedge fund assets appraised by Eshraghi & Taffler (2012) studied until June 2008 followed by subsequent dramatic collapse quoted through [16] underlying all financial innovations.

Referring to Maria Lopez Garcia & Jose Pedro Ramos Requena (2019) [4] about fractal market hypothesis, we found the case for the Helium Nat Gas Project is in the relation between probability & hypothesis. Also from Figure 1, the evolution from histogram between ‘a number of occurrence’ to Z, instead to bell-curve between Probability & ‘Size of Jump in market value’ as well as to ‘probability density function’ <-> profit, we found for Levy stable process.

Have been completed of reasons & descriptions of the hypothesis whereas fractal properties coincidence with the econophysics of the market, especially about helium extraction projects from natural gas. To conclude exergy conception also can be applied, we must make a specific & and whole study of calculations and assumptions to follow that have determined the limit of the economical value of helium extraction from nat gas (0.05% helium containing per gas well) before establishing the project.

Disclaimer

This chapter is an extended version of the article published by the same author(s) in the following journal. Journal of Oil and Gas Research Reviews, 3(2): 99, 2023.

Peer-review history

This chapter was reviewed by following the Advanced Open Peer Review policy. This chapter was thoroughly checked to prevent plagiarism. As per editorial policy, a minimum of two peer-reviewers reviewed the manuscript. After review and revision of the manuscript, the Book Editor approved the manuscript for final publication. Peer review comments, comments of the editor(s), etc. are available here:

1. Buratti C, Conti A, Dardari D, Verdone R. An overview on wireless sensor networks technology and evolution. Sensors. 2009;9(9):6869-6896. Available from: https://doi.org/10.3390/s90906869
2. Matin MA, Islam MM. Overview of wireless sensor network. Wireless Sensor Networks-Technology and Protocols. 2012;1(3). Available from: https://www.researchgate.net/publication/272832872_Overview_of_Wireless_Sensor_Network
3. Buchanan M. The physics of the trading floor. Nature. 2002;415 (6867):10-12. Available from: https://doi.org/10.1038/415010a
4. de Las Nieves Lopez Garcia M, Ramos Requena JP. Different methodologies & uses of the Hurst exponent in econophysics. Estudos de Economia Aplicada. 2019;37(2). Available from: https://doi.org/10.25115/eea.v37i2.2603
5. Tulusoy T, Sen AT. A sociophysical approach to relationship between politics and economy: The Lagrange model of the crowds. Quantrade Journal of Complex Systems in Social Sciences. 2019;1(1). Available from: https://dergipark.org.tr/en/download/article-file/885837
6. Maksoed WH. Enhanced & fractal involving of ‘Helium Nat Gas Project’ econophysics. J Oil Gas Res Rev. 2023;3(2):83-84. Available from: https://www.opastpublishers.com/peer-review/enhanced-fractal-involving-of-helium-nat-gas-project-econophysics-6349.html
7. Kuznetsov DV, Mandel I. Introduction to statistical physics of media processes: Mediaphysics. arXiv: physics/0506217v1; 2005. Available from: https://arxiv.org/abs/physics/0506217
8. Selvam AM. Fractal fluctuations & statistical normal distribution. Fractals. 2009;17(3):333-349. doi: 10.1142/S0218348X09004272. Available from: https://arxiv.org/pdf/0805.3426
9. Septiana R, Kartohardjono S. Techno-economic analysis of LNG boil-off gas treatment: A case study of LNG terminal in Indonesia. Int J Adv Sci Tech. 2020;29(4):2567-2578. Available from: https://www.researchgate.net/publication/342168675_Techno-Economic_Analysis_of_LNG_Boil-Off_Gas_Treatment_A_Case_Study_of_LNG_Terminal_in_Indonesia
10. Ilinski K. Physics of finance. arXiv/9710148v1; 1997. Available from: https://arxiv.org/abs/hep-th/9710148
11. Kachunni SK, Ghosh P, Chowdhury K. Optimization of UA of heat exchanger and BOG compressor exit pressure of LNG boil-off gas reliquefaction system using exergy analysis. IOP Conf Ser: Mater Sci Eng. 2015;101:012090. Available from: http://dx.doi.org/10.1088/1757-899X/101/1/012090
12. Liu G, Chih-Ping Yu, Shan-Neng Shiu, I-Tung Shih. The efficient market hypothesis & the fractal market hypothesis: Intrafluves, fusions & evolutions. SAGE-Journal. 2015;12(1). Available from: http://dx.doi.org/10.1177/21582440221082137
13. Weron A. Fractal market hypothesis and two power-laws. Chaos Solitons Fractals. 2000;11:289-296. Available from: https://prac.im.pwr.edu.pl/~hugo/publ/AWeronRWeron00_CSF.pdf
14. Mandelbrot BB. Fractals & scaling in finance. 1997.
15. Taheri K, Gadow R, Killinger A. Exergy analysis as a developed concept of energy efficiency optimized processes: The case of thermal spray processes. Science Direct. 2014;17:511-516. Available from: https://doi.org/10.1016/j.procir.2014.01.060
16. Hidajatullah-Maksoed W. Valuesale’ of helium extraction & on-purpose propylene processing from natural gas. Oil Gas Res Rev. 2023;9(4). Available from: https://www.researchgate.net/publication/373976642_Valuesale_of_Helium_Extraction_On-Purpose_Propylene_Processing_from_Natural_Gas